微分係数と接線

定義 3.8 (接線)   点 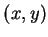$(x,y)$ における微分係数 $f'(x)$ を曲線 $y=f(x)$ の 接線（tangent）と呼ぶ．

点 $P(x,y)$, $Q(x+\Delta x,y+\Delta y)$, $R(x+\Delta x,y)$ からなる 三角形を考える． $\angle PRQ=\pi/2$ だからこの三角形は直角三角形である． $\angle QPR$ の角度を $\theta$ とおくと

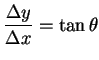$$\frac{\Delta y}{\Delta x}=\tan \theta$$ (259)

が成り立つ．斜辺 $PQ$ の傾きは $\tan\theta$ である． $\Delta x\to0$ のときの $\theta(x,\Delta x)$ の極限を考える． まず $\Delta y/\Delta x$ を計算すると

$$\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x\to0}\frac{\Delta y(x,\Delta x)}{\Delta x}= \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$ (260)

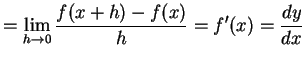$$= \lim_{h\to0}\frac{f(x+h)-f(x)}{h}= f'(x)= \frac{dy}{dx}$$ (261)

を得る． 傾き $\Delta y/\Delta x$ の極限が $f'(x)$ であるので， $\tan \theta(x,\Delta x)$ の極限も $f'(x)$ となる． よって $\Delta x\to0$ における $\theta(x,\Delta x)$ の極限 $\alpha(x)$ が存在し，

$$\lim_{\Delta x\to0}\tan\theta(x,\Delta x)= \lim_{\Delta x\to0}\frac{\Delta y}{\Delta x} \quad \to \quad \tan \alpha(x) = \frac{dy}{dx}=f'(x)$$ (262)

となる． 以上より， 点 $P(x,y)$ に接するように極微小な三角形を描いたとき， その斜辺の傾きは $\tan\alpha(x)$ であり， その角度は $\alpha(x)=\arctan f'(x)$ である．

例 3.9 (接線の方程式)   曲線 $y=f(x)$ 上の点 $(a,f(a))$ において 曲線に接する直線を接線と呼ぶ． 接線の方程式は

$$y=f(a)+f'(a)(x-a)$$ (263)

で与えられる． この方程式を導出する． 点 $(a,f(a))$ に接する極微小な直角三角形を考える． このとき三角形の斜辺の傾きは $\tan\alpha=f'(a)$ である． 次に極微小な三角形と相似で点 $(a,f(a))$, $(x,f(x))$ を 斜辺とする三角形を考える． この三角形の斜辺の傾き $(y-f(a))/(x-a)$ は 相似図形であるから， $\tan\alpha=f'(a)$ となる． よって

$$\frac{y-f(a)}{x-a}=\tan\alpha=f'(a)$$ (264)

が成り立つ． これより接線の方程式を得る． 接線の方程式は点 $x=a$ における関数 $f(x)$ の 1 次（線形）近似ともいう． ちなみに関数 $f(x)$ の $x=a$ における 0 次近似は $y=f(a)$ である．

問 3.10   教科書（p.46）問題 3-2.

Kondo Koichi
Created at 2002/09/12