Next: 対数関数の微分 Up: 微分法 Previous: 定数の微分 Contents
巾関数の微分
定理 3.16 (巾関数の微分)
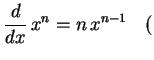 |
(292) |
問 3.17
これを示せ.
を得る.ここで
であることを用いると
となる.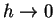 のとき
のとき
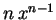 の項は生き残り,
その後ろの項は消える.
よって
の項は生き残り,
その後ろの項は消える.
よって
を得る.
(証明)
![]() とおき定義に従い計算すると,
とおき定義に従い計算すると,
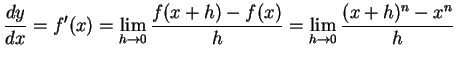 |
(293) |
を得る.ここで
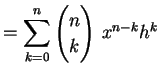 |
(294) | |
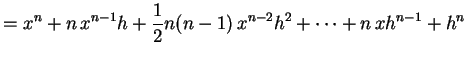 |
(295) | |
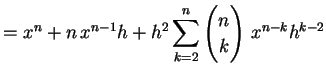 |
(296) |
であることを用いると
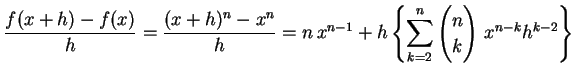 |
(297) |
となる.
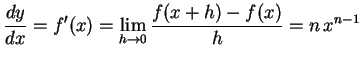 |
(298) |
を得る.
定理 3.18 (負巾関数の微分)
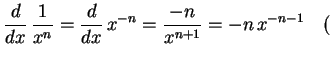 |
(299) |
問 3.19
これを示せ.
となる.これを用いて
を得る.
(証明)
![]() とおく.
このとき
とおく.
このとき
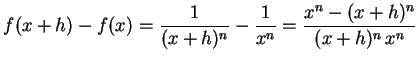 |
(300) | |
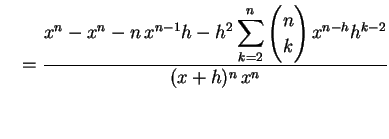 |
(301) | |
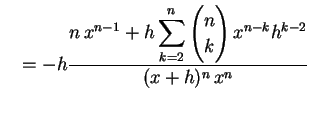 |
(302) |
となる.これを用いて
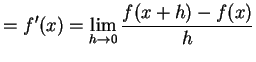 |
(303) | |
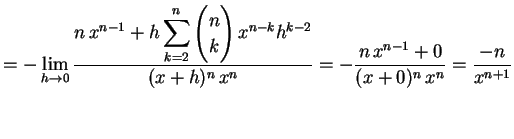 |
(304) |
を得る.
定理 3.20 (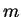 乗根関数の微分)
乗根関数の微分)
![$\displaystyle \frac{d}{dx}\,\sqrt[m]{x}= \frac{d}{dx}\,x^{\frac{1}{m}}= \frac{\sqrt[m]{x}}{m\,x}= \frac{1}{m}\,x^{\frac{1}{m}-1} \quad($](img717.png) |
(305) |
問 3.21
これを示せ.
である. ここで
であることを用いる.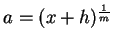 ,
,
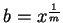 とおくと
とおくと
を得る.よって
となる.
(証明)
![]() とおく.
このとき
とおく.
このとき
| (306) |
である. ここで
| (307) | ||
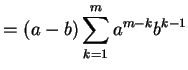 |
(308) | |
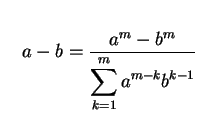 |
(309) |
であることを用いる.
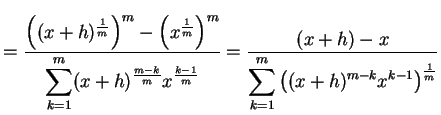 |
(310) | |
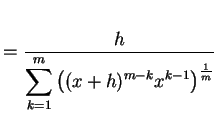 |
(311) |
を得る.よって
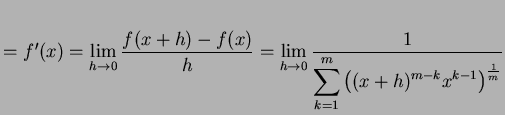 |
(312) | |
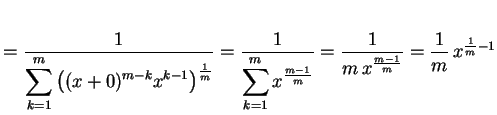 |
(313) |
となる.
定理 3.22 (巾関数の微分)
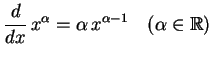 |
(314) |
Next: 対数関数の微分 Up: 微分法 Previous: 定数の微分 Contents
Kondo Koichi
Created at 2002/09/12