Next: 10 定積分 Up: 6 積分法 Previous: 8 三角関数の有理式の積分 Contents
9 漸化式を用いた積分の計算
例 6.31 (漸化式による不定積分の求積)
不定積分
を考える.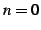 のとき
のとき
を得る.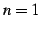 のとき
のとき
を得る.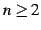 のときを考える.
のときを考える.
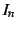 を部分積分を用いて計算すると
を部分積分を用いて計算すると
となる.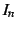 を移項すると
を移項すると
を得る. 最後の式は漸化式である. この漸化式より不定積分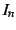 が求まる.
同様にして
が求まる.
同様にして
を得る.
| (958) | ||
| (959) |
を考える.
| (960) | ||
| (961) |
を得る.
| (962) | ||
| (963) |
を得る.
| (964) | ||
| (965) | ||
| (966) | ||
| (967) | ||
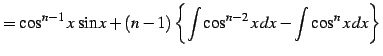 |
(968) | |
| (969) | ||
| (970) |
となる.
| (971) | ||
| (972) | ||
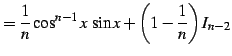 |
(973) |
を得る. 最後の式は漸化式である. この漸化式より不定積分
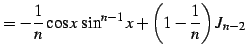 |
(974) |
を得る.
問 6.32 (漸化式による不定積分の求積)
 についての漸化式を求めよ.
についての漸化式を求めよ.
Next: 10 定積分 Up: 6 積分法 Previous: 8 三角関数の有理式の積分 Contents
Kondo Koichi

Created at 2004/08/14