6.3 2 次曲線の平行移動
定理 6.8 (2 次曲線の平行移動)
有心 2 次曲線
は平行移動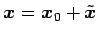 により,
により,
と表される.
と表される. これに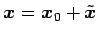 を代入すると
を代入すると
となる.ここで一般に
となるので,
と表される. ただし,
とおいた.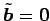 とおく.
とおく.
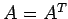 であることと
であることと 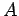 が正則であることに注意すると,
が正則であることに注意すると,
より,中心は
と得られる. 以上より, 平行移動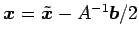 により
中心は原点に移り, 2 次曲線は
により
中心は原点に移り, 2 次曲線は
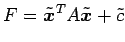 となる.
となる.
は平行移動
と表される.
(証明) 2 次曲線は
と表される. これに
となる.ここで一般に
となるので,
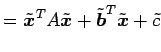 |
と表される. ただし,
とおいた.
より,中心は
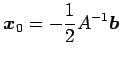 |
と得られる. 以上より, 平行移動
Kondo Koichi

平成18年1月17日