6.5 分類外の 2 次曲線
まとめ 6.14 (2 次曲線の分類)
2 次曲線は楕円,双曲線,放物線以外のグラフもありうる.
標準形の形で次のように分類される:
(i)
楕円:
![]() ,
,
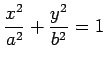 のとき.
のとき.
(ii)
点楕円:
![]() ,
,
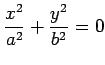 のとき,原点のみの楕円形.
のとき,原点のみの楕円形.
(iii)
虚の楕円:
![]() ,
,
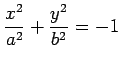 のとき,
のとき,
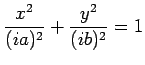 より
より
![]() ではグラフは存在しない.
ではグラフは存在しない.
(iv)
双曲線:
![]() ,
,
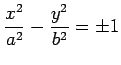 のとき.
のとき.
(v)
交わる 2 つの直線:
![]() ,
,
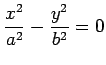 のとき,
のとき,
![]() と書き換えて 2 直線
と書き換えて 2 直線 ![]() ,
, ![]() となる.
となる.
(vi)
放物線:
![]() ,
,
![]() または
または
![]() のとき.
のとき.
(vii)
平行な 2 つの直線:
![]() ,
, ![]() または
または ![]() のとき.
のとき.
(viii)
重なった 1 つの直線:
![]() ,
, ![]() または
または ![]() のとき.
のとき.
(ix)
虚の平行 2 直線:
![]() ,
, ![]() または
または ![]() のとき.
のとき.
注意 6.15 (交わる 2 直線)
2 次曲線
は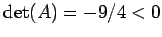 より双曲形であるが,
より双曲形であるが,
と因数分解されるので,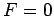 は 2 つの直線
は 2 つの直線
を表す.
は
と因数分解されるので,
を表す.
注意 6.16 (平行 2 直線)
2 次曲線
は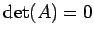 より無心 2 次曲線である.
より無心 2 次曲線である.
と因数分解されるので,2 つの平行な直線を表す.
は
と因数分解されるので,2 つの平行な直線を表す.
注意 6.17 (虚の直線)
2 次曲線 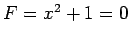 は
は
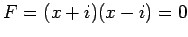 と書けるから,
2 つの虚の直線を表す.
よって,実数の範囲内ではグラフは存在しない.
と書けるから,
2 つの虚の直線を表す.
よって,実数の範囲内ではグラフは存在しない.
Kondo Koichi

平成18年1月17日