3.41 演習問題 〜 正規直交基底
問 3.161 (正規直交基底)
次の基底を正規直交化せよ.
(1)
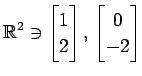 (2)
(2)
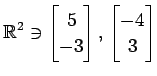 (3)
(3)
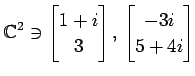
(4)
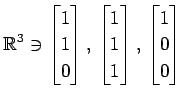 (5)
(5)
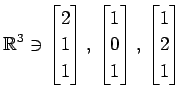 (6)
(6)
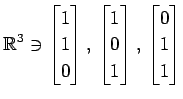
(7)
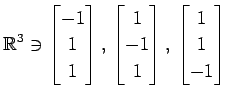 (8)
(8)
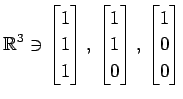 (9)
(9)
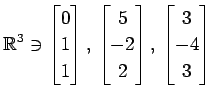
(10)
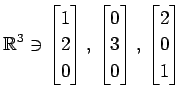 (11)
(11)
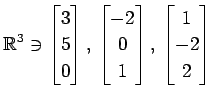 (12)
(12)
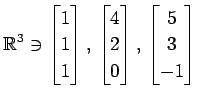
(13)
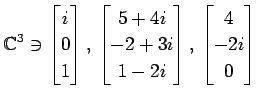 (14)
(14)
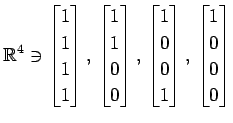
(15)
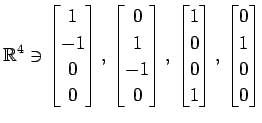 (16)
(16)
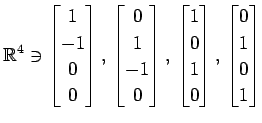
(17)
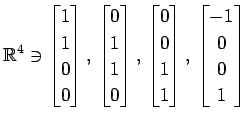 (18)
(18)
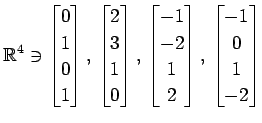
(19)
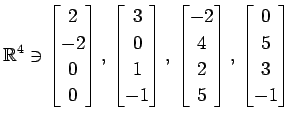 (20)
(20)
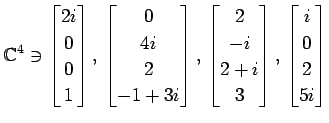
問 3.162 (正規直交基底)
前問で得た正規直交基底における次のベクトルの座標を求めよ.
(1)-(2)
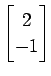 (3)
(3)
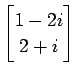 (4)-(12)
(4)-(12)
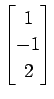 (13)
(13)
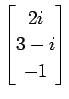 (14)-(19)
(14)-(19)
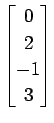
(20)

問 3.163 (グラム・シュミットの直交化法)
![$ \mathbb{R}[x]_2$](img410.png) の基底
(1)
の基底
(1)
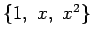 (2)
(2)
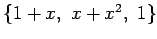 を正規直交化せよ.
ただし,内積は
を正規直交化せよ.
ただし,内積は
とする.
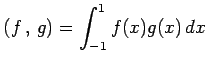 |
とする.
問 3.164 (グラム・シュミットの直交化法)
![$ \mathbb{R}[x]_n$](img373.png) の基底
の基底 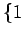 ,
, 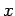 ,
, 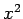 ,
, 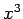 ,
, 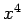 ,
, 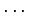 ,
, 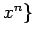 を
正規直交化せよ.
ただし,内積は前問と同じとする.
を
正規直交化せよ.
ただし,内積は前問と同じとする.
Kondo Koichi

平成18年1月17日