4.2 演習問題 〜 線形写像
(1)
点 ![]() と原点
と原点 ![]() との中点
との中点 ![]() への変換.
への変換.
(2)
点 ![]() と点
と点
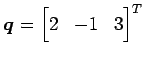 との中点
との中点 ![]() への変換.
への変換.
(3)
直線 ![]() を原点
を原点 ![]() を通り方向ベクトル
を通り方向ベクトル
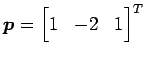 の
直線とする.
点
の
直線とする.
点 ![]() から直線
から直線 ![]() へ正射影
へ正射影 ![]() への変換.
への変換.
(4)
直線 ![]() を点
を点 ![]() を通り
方向ベクトル
を通り
方向ベクトル ![]() の直線とする.
点
の直線とする.
点 ![]() から直線
から直線 ![]() への正射影
への正射影 ![]() への変換.
への変換.
(5)
点 ![]() から直線
から直線 ![]() への正射影との中点
への正射影との中点 ![]() への変換.
への変換.
(6)
点 ![]() から直線
から直線 ![]() への正射影との中点
への正射影との中点 ![]() への変換.
への変換.
(7)
直線
![]() を原点
を原点 ![]() を通り方向ベクトル
を通り方向ベクトル
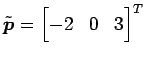 の
直線とする.
点
の
直線とする.
点 ![]() から直線
から直線 ![]() への正射影と
点
への正射影と
点 ![]() から直線
から直線
![]() への正射影との
中点
への正射影との
中点 ![]() への変換.
への変換.
(8)
直線
![]() を点
を点 ![]() を通り
方向ベクトル
を通り
方向ベクトル
![]() の直線とする.
点
の直線とする.
点 ![]() から直線
から直線 ![]() への正射影と
点
への正射影と
点 ![]() から直線
から直線
![]() への正射影との
中点
への正射影との
中点 ![]() への変換.
への変換.
(9)
![]() 平面への正射影
平面への正射影 ![]() への変換.
(10)
平面
への変換.
(10)
平面 ![]() への正射影
への正射影 ![]() への変換.
への変換.
(11)
![]() 平面への正射影
平面への正射影 ![]() への変換.
(12)
平面
への変換.
(12)
平面 ![]() への正射影
への正射影 ![]() への変換.
への変換.
(13)
![]() 平面への正射影との中点
平面への正射影との中点 ![]() への変換.
への変換.
(14)
平面 ![]() への正射影との中点
への正射影との中点 ![]() への変換.
への変換.
(15)
原点 ![]() に関して点対称な点
に関して点対称な点 ![]() への変換.
(16)
原点
への変換.
(16)
原点 ![]() に関して点対称な点
に関して点対称な点 ![]() への変換.
への変換.
(17)
![]() 平面に関して対称な点
平面に関して対称な点 ![]() への変換.
への変換.
(18)
平面 ![]() に関して対称な点
に関して対称な点 ![]() への変換.
への変換.
(19)
原点 ![]() と点
と点 ![]() を通る直線上にあり,
原点
を通る直線上にあり,
原点 ![]() からの距離が
からの距離が ![]() 倍となる点
倍となる点 ![]() への変換.
への変換.
(20)
点 ![]() と点
と点 ![]() を通る直線上にあり,
点
を通る直線上にあり,
点 ![]() からの距離が
からの距離が ![]() 倍となる点
倍となる点 ![]() への変換.
への変換.
(1)
![]() (2)
(2)
![]()
(3)
![]() (4)
(4)
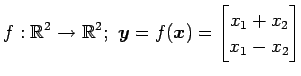
(5)
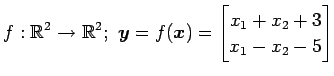 (6)
(6)

(7)
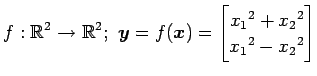 (8)
(8)
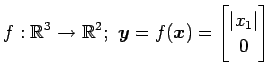
(9)
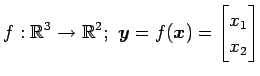 (10)
(10)
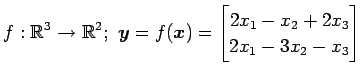
(11)
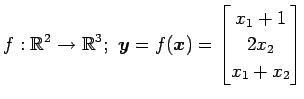 (12)
(12)
![]()
(13)
![]() (14)
(14)
![]()
(15)
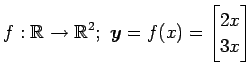 (16)
(16)
![]()
(17)
![]() ,
ただし
,
ただし
![]() .
.
(18)
![]() ,
ただし
,
ただし
![]() ,
,
![]() .
.
(19)
![]()
(20)
![]()
(21)
![]() ,
ただし
,
ただし
![]() .
.
(1)
![]() (2)
(2)
![]()
(3)
![]() (4)
(4)
![]()
(5)
![]()
などと表記する.
Kondo Koichi

平成18年1月17日