4.13 演習問題 〜 像,核,正則変換
問 4.61 (像,核,階数,退化次数)
次の写像の核と像の基底の組をそれぞれ求め,退化次数と階数を求めよ.
また,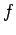 が正則であるか否か述べよ.
が正則であるか否か述べよ.
(1)
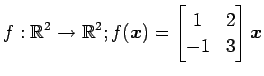 (2)
(2)
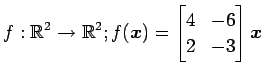
(3)
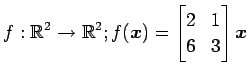 (4)
(4)
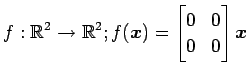
(5)
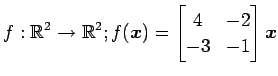 (6)
(6)
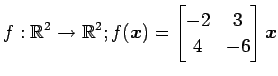
(7)
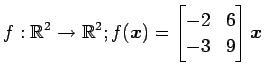 (8)
(8)
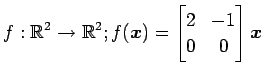
(9)
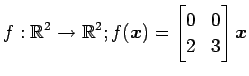 (10)
(10)
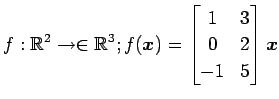
(11)
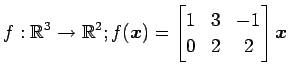 (12)
(12)
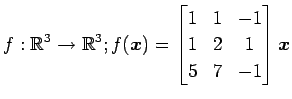
(13)
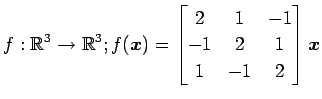 (14)
(14)
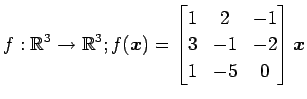
(15)
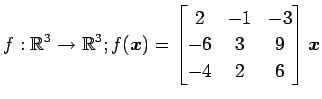 (16)
(16)
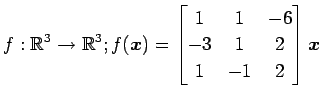
(17)
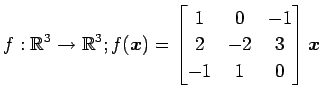 (18)
(18)
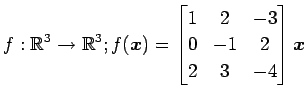
(19)
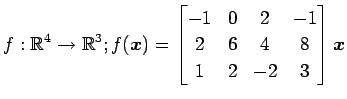 (20)
(20)
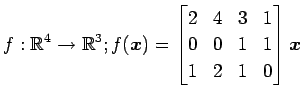
(21)
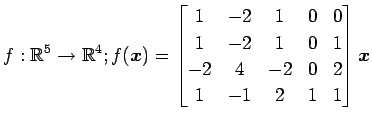
(22)
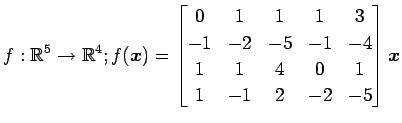
(23)
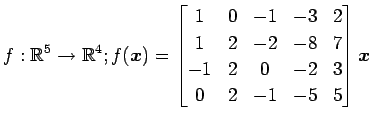
問 4.62 (線形変換の像,核,階数,退化次数)
「演習問題 〜 線形写像の表現行列」の
線形写像の像,核,階数,退化次数をそれぞれ求めよ.
また,写像が正則であるか否か述べよ.
問 4.63 (合成写像)
線形写像 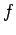 の表現行列を
の表現行列を 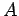 とし,
線形写像
とし,
線形写像 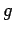 の表現行列を
の表現行列を 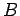 とする.
合成写像
とする.
合成写像 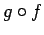 の表現行列を求めよ.
の表現行列を求めよ.
(1)
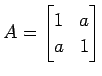 ,
,
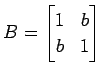 (2)
(2)
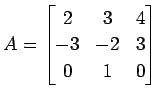 ,
,
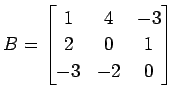
(3)
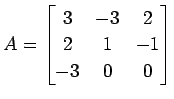 ,
,
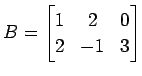
Kondo Koichi

平成18年1月17日