4.18 鏡映変換
例 4.82 (直交変換の具体例)
線形変換
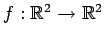 ;
;
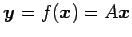 ,
,
を考える.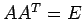 となるので
となるので 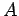 は直交行列である.
2 つのベクトル
は直交行列である.
2 つのベクトル
を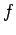 で写すと
で写すと
となる. このとき
となるから,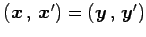 を得る.
よって
を得る.
よって 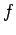 は直交変換である.
またこのとき,
は直交変換である.
またこのとき,
が成り立つ.
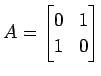 |
を考える.
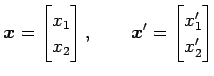 |
を
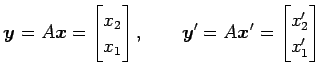 |
となる. このとき
となるから,
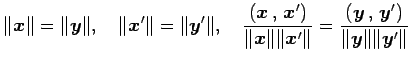 |
が成り立つ.
![]() は直線
は直線 ![]() に対する鏡映変換である.
に対する鏡映変換である.
例 4.83 (直交変換の具体例)
直交変換
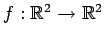 ;
;
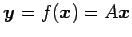 ,
,
は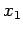 軸に対する鏡映変換である.
軸に対する鏡映変換である.
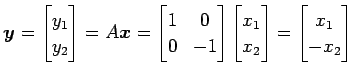 |
は
Kondo Koichi

平成18年1月17日