3.23 演習 〜 初等関数
問 3.72 (関数の種類)
次の写像(1)-(3)は,単射(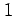 対
対 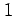 写像),全射(上への写像),
全単射(上への
写像),全射(上への写像),
全単射(上への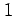 対
対 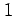 写像),いずれでもない,のどれであるか答えよ.
写像),いずれでもない,のどれであるか答えよ.
(1)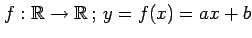 (2)
(2)
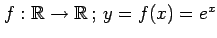
(3)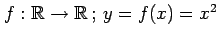
(1)
(3)
問 3.73 (逆関数)
次の関数  の逆関数
の逆関数
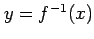 を求めよ.
また,これらのグラフを描け.
を求めよ.
また,これらのグラフを描け.
(1) (2)
(2)
 (3)
(3)
 (4)
(4)

(5) (6)
(6)
 (7)
(7)

(8)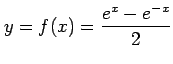
(1)

(5)

(8)
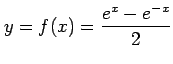
問 3.74 (三角関数)
次の値を求めよ.
(1)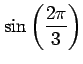 (2)
(2)
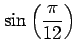 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
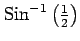
(7) (8)
(8)
 (9)
(9)
 (10)
(10)
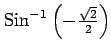 (11)
(11)

(12) (13)
(13)
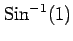 (14)
(14)
 (15)
(15)
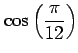 (16)
(16)

(17)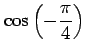 (18)
(18)
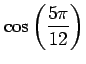 (19)
(19)
 (20)
(20)
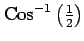 (21)
(21)
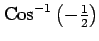
(22) (23)
(23)
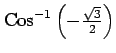 (24)
(24)
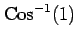 (25)
(25)
 (26)
(26)
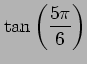
(27) (28)
(28)
 (29)
(29)
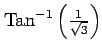 (30)
(30)
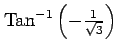 (31)
(31)
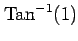
(32)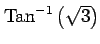 (33)
(33)
 (34)
(34) 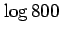 (
(
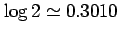 を用いよ)
を用いよ)
(1)
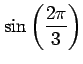 (2)
(2)
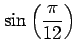 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
(7)
 (10)
(10)
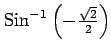 (11)
(11)

(12)
 (13)
(13)
 (15)
(15)
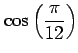 (16)
(16)

(17)
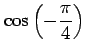 (18)
(18)
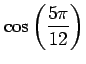 (19)
(19)
(22)
 (23)
(23)
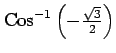 (24)
(24)
 (26)
(26)
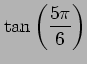
(27)
 (28)
(28)
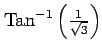 (30)
(30)
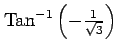 (31)
(31)
(32)
問 3.75 (三角関数)
 ,
,
 (ヒント:右辺に加法公式)
(ヒント:右辺に加法公式)
 (ヒント:右辺に加法公式)
(ヒント:右辺に加法公式)
問 3.76 (三角関数)
次の条件をみたす係数
 を求めよ.
を求めよ.
(1)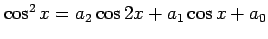
(2)
(3)
(1)
(2)
(3)
問 3.77 (双曲線関数)
双曲線関数  ,
,
 ,
,
 の定義を書け.
の定義を書け.
問 3.78 (双曲線関数)
次の問に答えよ.
(1) 双曲線関数 の定義を書け.
の定義を書け.
(2) 双曲線関数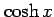 の逆関数
の逆関数
 を対数関数で表せ.
を対数関数で表せ.
(3) 加法公式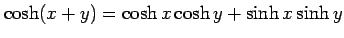 を証明せよ.
を証明せよ.
(1) 双曲線関数
(2) 双曲線関数
(3) 加法公式
問 3.79 (双曲線関数)
次の等式を証明せよ.
(1) (2)
(2)

(3)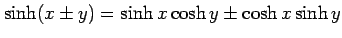 (4)
(4)

(5)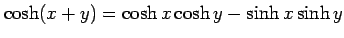 (6)
(6)

(7)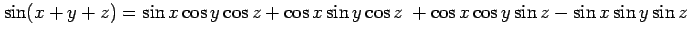
(8)
(ヒント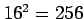 ,
,  ,
,  )
)
(9)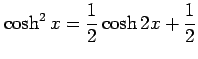 (10)
(10)

(1)
(3)
(5)

(7)
(8)

(ヒント
(9)
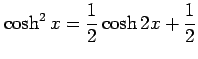 (10)
(10)

問 3.80 (双曲線関数)
 を任意の実数とするとき,
を任意の実数とするとき,
 ,
,
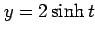 をみたす
をみたす 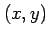 のグラフを描け.
のグラフを描け.
問 3.81 (関数の性質)
関数  は
は 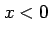 において単調減少であり,
において単調減少であり,
 において単調増加であることを示せ.
において単調増加であることを示せ.
問 3.82 (関数の性質)
次の関数についてグラフを描け.また下記の表を埋めよ.
(i)-(iv)についても述べよ.
(i)定義域と値域を述べよ.
(ii)多価関数であるか述べよ.また多価関数である場合は何価であるか述べよ.
(iii)周期関数の場合はその周期を述べよ.
(iv)偶関数または奇関数である場合はその種別を述べよ.
(1)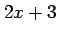 の逆関数
(2)
の逆関数
(2)  の逆関数
(3)
の逆関数
(3) 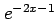 の逆関数
(4)
の逆関数
(4)  の逆関数
の逆関数
(5)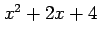 の逆関数
(6)
の逆関数
(6)
 の逆関数
(7)
の逆関数
(7)  (8)
(8) 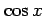 (9)
(9) 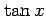 (10)
(10)

(11)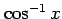 (12)
(12)
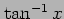 (13)
(13)
 (14)
(14)
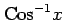 (15)
(15)
 (16)
(16) 
(17)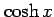 (18)
(18)  (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
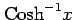
(23) (24)
(24)
 (25)
(25)
 (26)
(26)
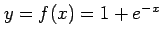 (27)
(27) 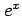
(28) (29)
(29)
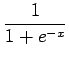 (30)
(30) 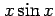 (31)
(31) 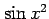
(注1)周期関数である場合は周期の値を書き, 周期関数ではない場合は×とする.
(注2)偶関数である場合は偶,奇関数である場合は奇, どちらでもない場合は×と書く.
(i)-(iv)についても述べよ.
(i)定義域と値域を述べよ.
(ii)多価関数であるか述べよ.また多価関数である場合は何価であるか述べよ.
(iii)周期関数の場合はその周期を述べよ.
(iv)偶関数または奇関数である場合はその種別を述べよ.
(1)
(5)
 の逆関数
(7)
の逆関数
(7) (11)
(17)
(23)
 (26)
(26)
(28)
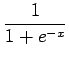 (30)
(30) | 問題 | 定義域 | 値域 | 価数 | 周期 (注1) | 偶・奇関数 (注2) |
| (例1) |
|
 |
2価 | 周期 |
奇 |
| (例2) |
|
|
1価 | 周期 |
偶 |
| (例3) |
|
|
無限多価 | |
|
| (1) | |||||
| (2) | |||||
| (3) | |||||
| (4) | |||||
| (5) | |||||
| (6) | |||||
| (7) | |||||
| (8) | |||||
| (9) | |||||
| (10) | |||||
| (11) | |||||
| (12) | |||||
| (13) | |||||
| (14) | |||||
| (15) | |||||
| (16) | |||||
| (17) | |||||
| (18) | |||||
| (19) | |||||
| (20) | |||||
| (21) | |||||
| (22) | |||||
| (23) | |||||
| (24) | |||||
| (25) | |||||
| (26) | |||||
| (27) | |||||
| (28) | |||||
| (29) | |||||
| (30) | |||||
| (31) |
(注1)周期関数である場合は周期の値を書き, 周期関数ではない場合は×とする.
(注2)偶関数である場合は偶,奇関数である場合は奇, どちらでもない場合は×と書く.
Kondo Koichi

平成19年1月23日