5.12 テイラー級数の計算
例 5.25 (テイラー級数の計算例)
 |
||
 |
||
例 5.26 (テイラー級数の計算例)
 |
||
 |
||
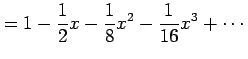 |
||
 |
||
 |
||
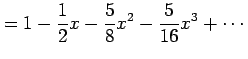 |
例 5.27 (テイラー級数の計算例)
 |
||
 |
||
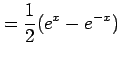 |
||
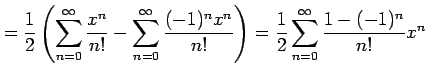 |
||
 |
||
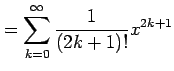 |
||
 |
問 5.28 (テイラー級数の計算)
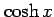 のテイラー級数を求めよ.
のテイラー級数を求めよ.
Kondo Koichi

平成19年1月23日