2.14 全微分と偏微分
定理 2.59 (全微分可能の必要条件)
関数  が全微分可能であれば,
が全微分可能であれば,
 は偏微分可能であり,
は偏微分可能であり,
が成り立つ.
が成り立つ.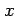 軸に沿って極限をとる.
軸に沿って極限をとる.
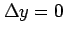 ,
,
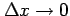 とする.
このとき,
とする.
このとき,
 であるから,
であるから,
が成り立つ. これは
と等価である. また, 軸に沿って極限をとる.
軸に沿って極限をとる.
 ,
,
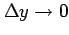 とすると,
同様にして
とすると,
同様にして
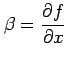 を得る.
を得る.
 |
が成り立つ.
(証明)
関数 ![]() が全微分可能であれば,
が全微分可能であれば,
が成り立つ.
が成り立つ. これは
 |
||
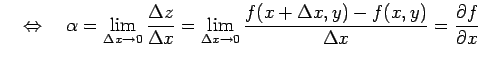 |
と等価である. また,
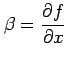 を得る.
を得る.
定理 2.60 (全微分可能の十分条件)
関数  において,
偏導関数
において,
偏導関数 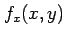 ,
,  が存在し,
かつこれらが連続関数であれば,
が存在し,
かつこれらが連続関数であれば,
 は全微分可能である.
(注意)逆は成り立たない.
は全微分可能である.
(注意)逆は成り立たない.
注意 2.61 (全微分可能の十分条件)
全微分可能となる十分条件は他にもあるが,
上の定理が一番実用的である.
例 2.62 (全微分)
関数
 は
偏導関数
は
偏導関数
が存在し,これらは連続関数である. よって は全微分可能である.
また,
は全微分可能である.
また,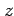 の全微分は
の全微分は
となる. (注意)微分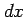 ,
,  と関数
と関数 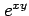 ,
, 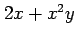 ,
, 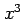 の
書く順を入れ替えてはならない.
つまり,
の
書く順を入れ替えてはならない.
つまり,
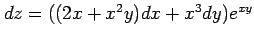 や
や
 は
誤った表記である.
は
誤った表記である.
が存在し,これらは連続関数である. よって
となる. (注意)微分
例 2.63 (全微分)
関数
 は
偏導関数
は
偏導関数
が存在し,かつこれらは連続関数である. よって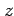 は全微分可能であり,
は全微分可能であり,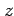 の全微分は
の全微分は
となる.
が存在し,かつこれらは連続関数である. よって
となる.
例 2.64 (全微分)
関数
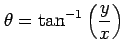 は
偏導関数
は
偏導関数
が存在し,かつこれらは原点を除き連続関数である. よって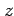 は原点を除き全微分可能であり,
は原点を除き全微分可能であり,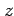 の全微分は
の全微分は
となる. (注意)微分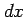 ,
,  と関数
と関数 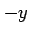 ,
, 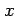 の
書く順を入れ替えてはならない.
また,分母
の
書く順を入れ替えてはならない.
また,分母  の部分は微分
の部分は微分 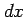 ,
,  の
前から
の
前から
 が掛けられているという意味で
あることに注意する.
つまり,以下の表記はすべて誤った表記である:
が掛けられているという意味で
あることに注意する.
つまり,以下の表記はすべて誤った表記である:
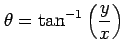 は
偏導関数
は
偏導関数
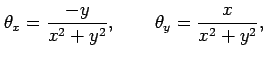 |
が存在し,かつこれらは原点を除き連続関数である. よって
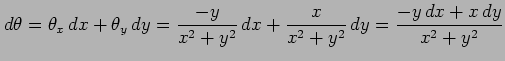 |
となる. (注意)微分
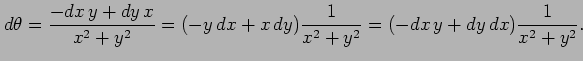 |
例 2.65 (全微分)
関数
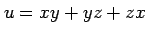 は
偏導関数
は
偏導関数
が存在し,かつこれらは連続関数である. よって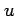 は全微分可能であり,
は全微分可能であり,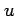 の全微分は
の全微分は
となる.
が存在し,かつこれらは連続関数である. よって
となる.
問 2.66 (全微分)
次の関数の全微分を求めよ.
Kondo Koichi

平成19年1月23日