3.20 線積分と多重積分
注意 3.92 (周回積分)
積分路 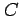 が一周しているとき,
線積分
が一周しているとき,
線積分
 を
を
と表記することがある. これを周回積分とも呼ぶ.
 を
を
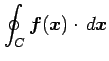 |
と表記することがある. これを周回積分とも呼ぶ.
定義 3.93 (領域の境界)
領域  の境界を
の境界を
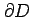 と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで
と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで 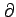 は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
定理 3.94 (グリーンの定理)
領域  内で関数
内で関数
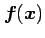 が連続なとき,
が連続なとき,
が成り立つ.
であるとき,
が成り立つ. 任意に与えられた領域を に関して単純な領域として分割し,
積分を求める.このとき重なり合う境界は向きが異なるので,
積分値は符号が反転し相殺しあう.
よって,任意の領域に対しても上式が成立する.
同様にして
に関して単純な領域として分割し,
積分を求める.このとき重なり合う境界は向きが異なるので,
積分値は符号が反転し相殺しあう.
よって,任意の領域に対しても上式が成立する.
同様にして  が
が  に関して単純な領域であるとすると
に関して単純な領域であるとすると
が成り立つ.これらを合わせてグリーンの定理を得る.
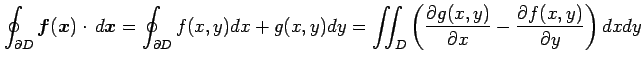 |
が成り立つ.
(証明)
![]() が
が ![]() に関して単純な領域
に関して単純な領域
であるとき,
 |
||
 |
||
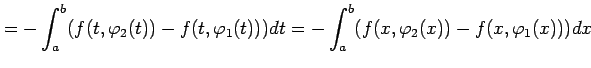 |
||
 |
||
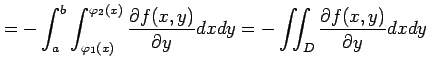 |
が成り立つ. 任意に与えられた領域を
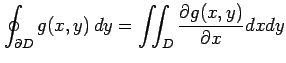 |
が成り立つ.これらを合わせてグリーンの定理を得る.
注意 3.95 (グリーンの定理)
グリーンの定理は線積分と多重積分の移り合いを表す.
例 3.96 (グリーンの定理の使用例)
 を半径
を半径 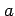 の円上を 1 周する有向曲線
の円上を 1 周する有向曲線
とする. このとき の内部の領域は
の内部の領域は
である. 領域 において関数
において関数  ,
, 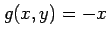 は連続であるから,
線積分
は連続であるから,
線積分
はグリーンの定理が適用でき,
と計算される.
とする. このとき
である. 領域
 |
はグリーンの定理が適用でき,
 |
と計算される.
例 3.97 (グリーンの定理が使用不可な例)
線積分
を考える. は単位円上を 1 周する有向曲線であり,
は単位円上を 1 周する有向曲線であり,
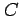 の内部の領域は
の内部の領域は
である. 関数
は原点で連続ではないので, 領域 のすべての点において
関数
のすべての点において
関数  ,
, 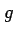 は連続ではないからグリーンの定理は適用できない.
は連続ではないからグリーンの定理は適用できない.
より,
となる. 正しくは,
と得られる.
 |
を考える.
である. 関数
 |
は原点で連続ではないので, 領域
誤りではあるが, グリーンの定理を適用して計算すると,
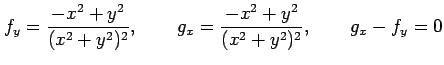 |
より,
 |
となる. 正しくは,
 |
||
 |
と得られる.
Kondo Koichi

平成19年1月23日