5.26 実標準形
実行列
![]() が複素固有値
が複素固有値 ![]() を
もつとき,その複素共役
を
もつとき,その複素共役
![]() も固有値となる.
なぜなら,固有多項式
も固有値となる.
なぜなら,固有多項式 ![]() は実係数であるから,
は実係数であるから,
![]() のとき
のとき
![]() が成り立つからである.
固有値
が成り立つからである.
固有値 ![]() に属する固有ベクトルを
に属する固有ベクトルを ![]() とすると
とすると
![]() である.
複素共役をとると
である.
複素共役をとると
![]() となるので,
となるので,
![]() に属する固有値ベクトルは
に属する固有値ベクトルは
![]() となる.
よって
となる.
よって
である. これより
 |
||
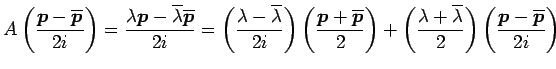 |
が成り立つ. 複素数
 ,
虚部を
,
虚部を
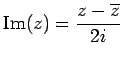 とおき,
ベクトル
とおき,
ベクトル を得る.
 |
が成り立つ.
定理 5.76 (実標準形)
実行列
 は
複素数体上で対角化可能であるとする.
固有値を
は
複素数体上で対角化可能であるとする.
固有値を
とし,それに属する固有ベクトルを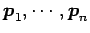 とする.
このとき,行列
とする.
このとき,行列 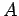 は
は
と実数体上でブロック対角化される. を実標準形(real canonical form???)という.
を実標準形(real canonical form???)という.
とし,それに属する固有ベクトルを
![$\displaystyle D= \begin{bmatrix}R(\lambda_1)\!\! \\ [-.8ex] & \!\!R(\lambda_2)\...
...athrm{Im}(\lambda) \\ \mathrm{Im}(\lambda) & \mathrm{Re}(\lambda) \end{bmatrix}$](img3378.png) |
||
 |
と実数体上でブロック対角化される.
例 5.77 (実標準形の具体例)
行列
の固有多項式は
であるから, 固有値は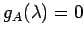 より,
より,
と複素数になる. それぞれの固有ベクトルは
より,
となる. よって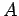 を複素数体上で対角化すると
を複素数体上で対角化すると
を得る. 次に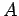 を実数体上で実標準形に分解する.
を実数体上で実標準形に分解する.
 ,
,
 となることに注意すると
となることに注意すると
を得る. 行列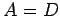 ,
, 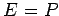 となることから,
となることから,
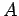 は既に実標準形のかたちをしている.
は既に実標準形のかたちをしている.
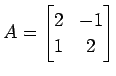 |
の固有多項式は
 |
であるから, 固有値は
と複素数になる. それぞれの固有ベクトルは
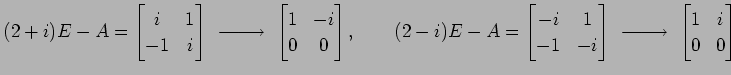 |
より,
 |
となる. よって
 |
||
 |
を得る. 次に
 |
||
 |
を得る. 行列
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日