3.30 次元と同じ個数の 1 次独立なベクトルは基底
定理 3.121 (ベクトルで張られる空間の次元)
ベクトル空間  の次元が
の次元が  のとき,
ベクトル
のとき,
ベクトル 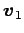 ,
, 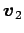 ,
, 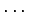 ,
,
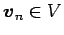 に対して
次の条件は等価である.
に対して
次の条件は等価である.
- (i).
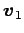 ,
, 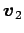 ,
, 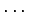 ,
, 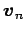 は
は  の基底である.
の基底である.
- (ii).
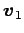 ,
, 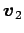 ,
, 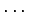 ,
, 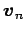 は 1 次独立である.
は 1 次独立である.
- (iii).
-
 .
.
例 3.122 (ベクトルで張られる空間の次元)
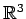 の基底のひとつに標準基底
の基底のひとつに標準基底
 がある.
個数は 3 個なので
がある.
個数は 3 個なので
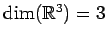 となる.
次に次元
となる.
次に次元
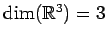 と同じ個数のベクトル
と同じ個数のベクトル
を考える. これらを列ベクトルとする行列を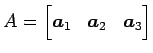 とおく.
とおく.
 より
より 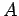 は正則となり,
ベクトルの組
は正則となり,
ベクトルの組
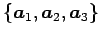 は
1 次独立である.
このとき
は
1 次独立である.
このとき
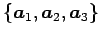 は基底となる.
これを示す.
は基底となる.
これを示す.
 の任意のベクトルは
の任意のベクトルは
と表される. ここで とおいた.
とおいた.
 ,
,
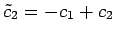 ,
,
 は任意の実数となる.
よって
は任意の実数となる.
よって
が成り立つ.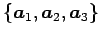 は 1 次独立であり
は 1 次独立であり
 を生成するので,
を生成するので,
 の基底となる.
の基底となる.
 |
を考える. これらを列ベクトルとする行列を
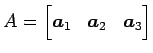 とおく.
とおく.
 |
||
 |
と表される. ここで
が成り立つ.
例 3.123 (ベクトルで張られる空間の次元)
![$ \mathbb{R}[x]_2$](img410.png) の基底のひとつに
の基底のひとつに
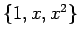 がある.
すなわち
がある.
すなわち
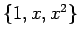 は 1 次独立であり
は 1 次独立であり
が成り立つ. よって![$ \dim(\mathbb{R}[x]_2)=3$](img1404.png) となる.
次に次元
となる.
次に次元
![$ \dim(\mathbb{R}[x]_2)=3$](img1404.png) と同じ個数のベクトル
と同じ個数のベクトル
を考える. これらのベクトルは
をみたす. であり
であり  は正則であるので,
ベクトルの組
は正則であるので,
ベクトルの組
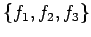 は 1 次独立となる.
このとき
は 1 次独立となる.
このとき
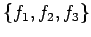 は基底となる.
これを示す.
は基底となる.
これを示す.
 に対して右から
に対して右から 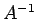 をかけると
をかけると
が成り立つ.![$ \mathbb{R}[x]_2$](img410.png) の任意のベクトルは
の任意のベクトルは
となる. ここで とおいた.
とおいた.
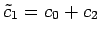 ,
,
 ,
,
 は任意の実数であるから,
は任意の実数であるから,
が成り立つ.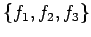 は一次独立であり
は一次独立であり
![$ \mathbb{R}[x]_2$](img410.png) を生成するので,
を生成するので,
![$ \mathbb{R}[x]_2$](img410.png) の基底となる.
の基底となる.
が成り立つ. よって
を考える. これらのベクトルは
 |
をみたす.
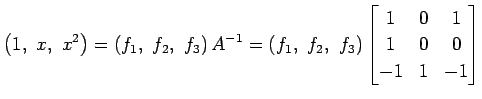 |
が成り立つ.
 |
||
となる. ここで
が成り立つ.
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日