3.40 グラム・シュミットの直交化法
定義 3.163 (正規直交化)
内積空間  において,基底
において,基底
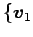 ,
,
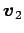 ,
, 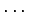 ,
,
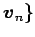 を基底
を基底
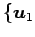 ,
,
 ,
, 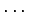 ,
,
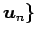 に取り替える.
このとき
に取り替える.
このとき
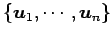 が正規基底となるとき,
この操作を正規化(normalize)という.
直交基底となるとき,直交化(orthogonalize)という.
正規直交基底となるとき,正規直交化(orthonormalize)という.
が正規基底となるとき,
この操作を正規化(normalize)という.
直交基底となるとき,直交化(orthogonalize)という.
正規直交基底となるとき,正規直交化(orthonormalize)という.
定理 3.164 (正規化)
内積空間  の
基底
の
基底
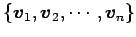 に対して
次の式で定まる
に対して
次の式で定まる
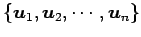 は
正規基底となる:
は
正規基底となる:
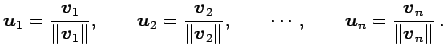 |
定理 3.165 (グラム・シュミットの直交化法)
内積空間  の基底
の基底
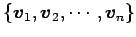 に
対して次の式で定まる
に
対して次の式で定まる
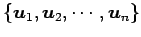 は
は
 の正規直交基底となる.
この手法を
グラム・シュミットの直交化法(Gram-Schmidt orthogonalization)
という.
の正規直交基底となる.
この手法を
グラム・シュミットの直交化法(Gram-Schmidt orthogonalization)
という.
以下同様.
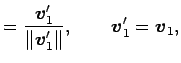 |
||
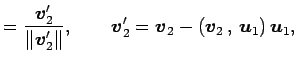 |
||
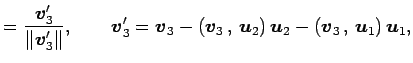 |
||
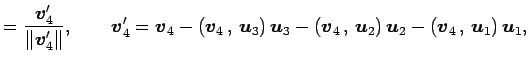 |
||
 |
||
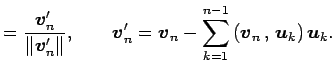 |
(証明)
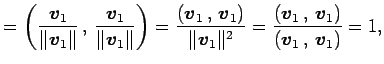 |
||
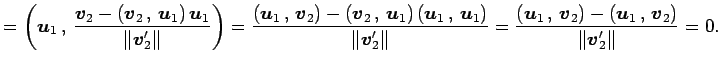 |
以下同様.
例 3.166 (グラム・シュミットの直交化法の具体例)
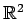 の基底
の基底
を正規直交化する. グラム・シュミットの直交化法より,
となる. 以上より
は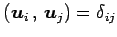 をみたし,
をみたし,
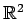 の正規直交基底となる.
の正規直交基底となる.
 |
を正規直交化する. グラム・シュミットの直交化法より,
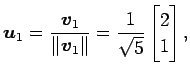 |
||
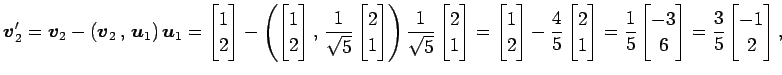 |
||
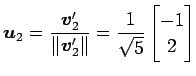 |
となる. 以上より
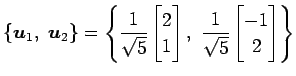 |
は
例 3.167 (グラム・シュミットの直交化法の具体例)
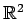 の基底
の基底
を正規直交化する. グラム・シュミットの直交化法より,
となる. 以上より
は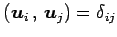 をみたし,
をみたし,
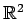 の正規直交基底となる.
の正規直交基底となる.
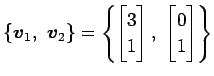 |
を正規直交化する. グラム・シュミットの直交化法より,
 |
||
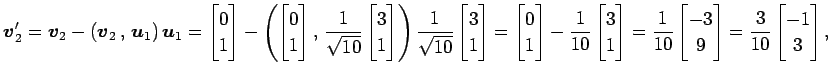 |
||
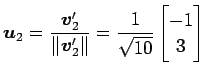 |
となる. 以上より
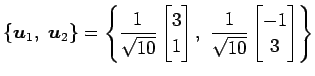 |
は
例 3.168 (グラム・シュミットの直交化法の具体例)
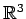 の基底
の基底
を正規直交化する. グラム・シュミットの直交化法より,
となる. 以上より
は
をみたし,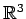 の正規直交基底となる.
の正規直交基底となる.
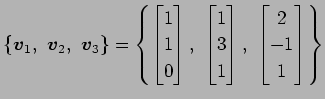 |
を正規直交化する. グラム・シュミットの直交化法より,
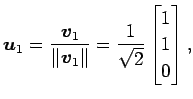 |
||
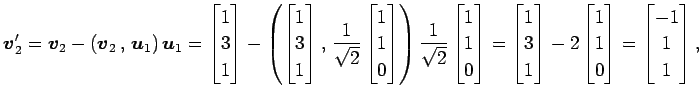 |
||
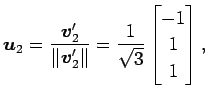 |
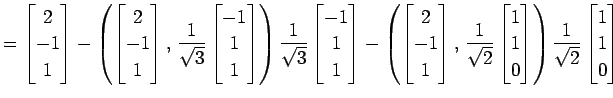 |
||
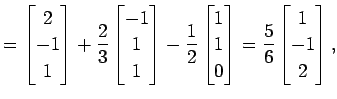 |
||
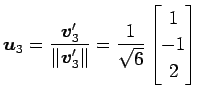 |
となる. 以上より
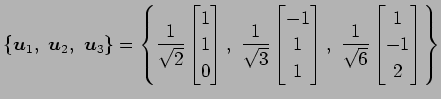 |
は
をみたし,
問 3.169 (グラム・シュミットの直交化法の具体例)
![$ \mathbb{R}[x]_n$](img373.png) の基底
の基底 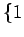 ,
, 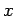 ,
, 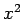 ,
,  ,
, 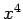 ,
, 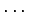 ,
, 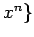 を
グラム・シュミットの直交化法で正規直交化せよ.
ただし,内積は
を
グラム・シュミットの直交化法で正規直交化せよ.
ただし,内積は
とする.
であるから,まず,
とおく.次に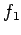 と
と 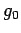 の内積は
の内積は
であるから,これらは直交しない. ここで
とおくと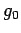 と
と
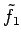 は直交する.
は直交する.
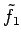 のノルムは
のノルムは
である.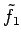 を正規化すると
を正規化すると
となる.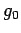 と
と 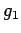 とは正規直交系である.
以下
とは正規直交系である.
以下 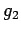 ,
, 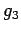 ,
, 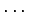 は自習.
は自習.
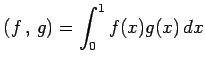 |
とする.
(答え)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() とおく.
とおく.
![]() のノルムは
のノルムは
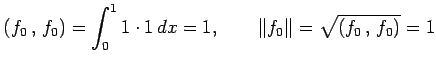 |
であるから,まず,
 |
とおく.次に
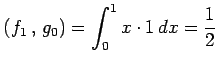 |
であるから,これらは直交しない. ここで
 |
とおくと
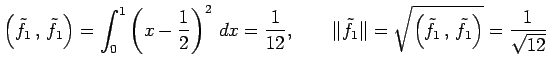 |
である.
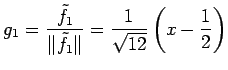 |
となる.
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日