5.24 演習 〜 テイラー展開
問 5.61 (テイラー級数)
関数  に関して点
に関して点 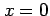 まわりでのテイラー級数を書け.
このとき
まわりでのテイラー級数を書け.
このとき 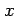 が収束する範囲も書くこと.
が収束する範囲も書くこと.
(1)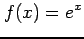 (2)
(2)
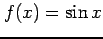 (3)
(3)
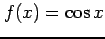 (4)
(4)
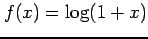 (5)
(5)
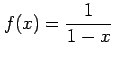
(6)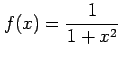 (7)
(7)
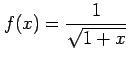 (8)
(8)
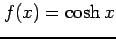 (9)
(9)
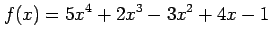
(10)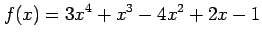 (11)
(11)
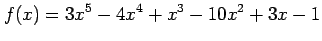
(12)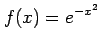 (13)
(13)
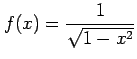
(1)
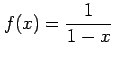
(6)
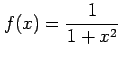 (7)
(7)
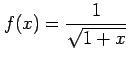 (8)
(8)
(10)
(12)
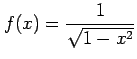
問 5.62 (テイラー級数展開による近似)
関数(1)
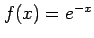 , (2)
, (2)
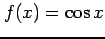 の近似を考える.
の近似を考える.
(i) 関数 を点
を点 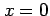 のまわりで点
のまわりで点 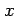 について有限テイラー展開せよ.
について有限テイラー展開せよ.
(ii) 関数 を原点の近くで多項式で近似せよ.0
次から
を原点の近くで多項式で近似せよ.0
次から 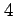 次の近似多項式
次の近似多項式
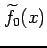 ,
,
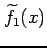 ,
, 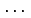 ,
,
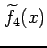 を求めよ.
を求めよ.
(iii) 点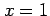 での近似多項式
での近似多項式
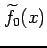 ,
, 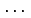 ,
,
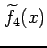 の誤差を評価せよ.
の誤差を評価せよ.
(iv)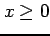 の範囲で近似多項式
の範囲で近似多項式
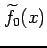 ,
, 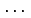 ,
,
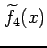 の誤差が
の誤差が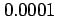 未満となる
未満となる 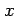 の範囲を求めよ.
の範囲を求めよ.
(i) 関数
(ii) 関数
(iii) 点
(iv)
問 5.63 (合成によるテイラー展開の計算)
次の関数のマクローリン級数を求めよ.
(注意:0
ではない最初の 4 項のみでよい.収束の範囲も特に書く必要なし.)
(1)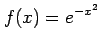 (2)
(2)
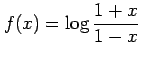 (3)
(3)
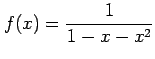 (4)
(4)
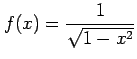
(5)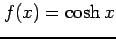 (6)
(6)
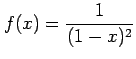 (7)
(7)
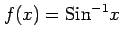 (8)
(8)
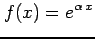 (9)
(9)
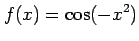
(10)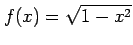
(1)
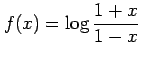 (3)
(3)
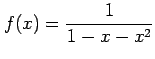 (4)
(4)
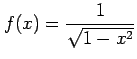
(5)
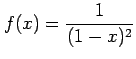 (7)
(7)
(10)
問 5.64 (項別微分)
関数
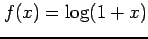 のマクローリン級数の項別微分が
関数
のマクローリン級数の項別微分が
関数
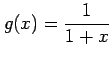 のマクローリン級数に等しいことを示せ.
のマクローリン級数に等しいことを示せ.
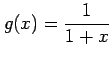 のマクローリン級数に等しいことを示せ.
のマクローリン級数に等しいことを示せ.
問 5.65 (テイラー展開とグラフの形)
関数
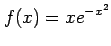 について
(i)
について
(i) が増加の状態,減少の状態となる
が増加の状態,減少の状態となる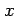 の範囲を求めよ.
の範囲を求めよ.
(ii) が極大値,極小値,変曲点をとる
が極大値,極小値,変曲点をとる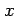 の点を求めよ.
(iii)
の点を求めよ.
(iii) のグラフの概形を描け.
のグラフの概形を描け.
(ii)
問 5.66 (テイラー展開を用いた極限の計算)
次の極限をテイラー級数展開を用いて求めよ.
(1)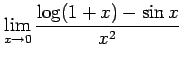 (2)
(2)
![$ \displaystyle{\lim_{x \to \infty}\left(\sqrt[3]{x^3+x^2}-x\right)}$](img2167.png) (3)
(3)
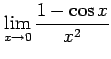 (4)
(4)
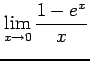
(5)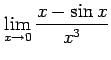 (6)
(6)
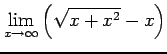
(1)
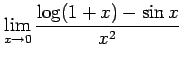 (2)
(2)
![$ \displaystyle{\lim_{x \to \infty}\left(\sqrt[3]{x^3+x^2}-x\right)}$](img2167.png) (3)
(3)
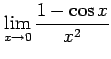 (4)
(4)
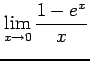
(5)
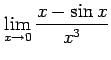 (6)
(6)
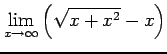
平成19年10月3日