6.15 定積分の置換積分
定理 6.74 (置換積分)
積分変数を 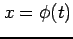 と置き換えると定積分は
と置き換えると定積分は
と表される.
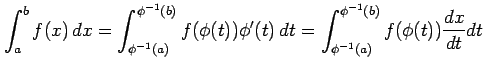 |
と表される.
例 6.75 (置換積分の計算例)
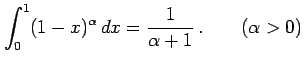 |
例 6.76 (置換積分の計算例)
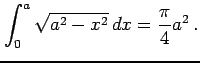 |
例 6.77 (置換積分の計算例)
ここで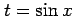 とおいた.このとき
とおいた.このとき
であることを用いた. また積分区間は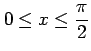 から
から
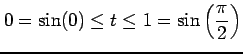 へと変わる.
へと変わる.
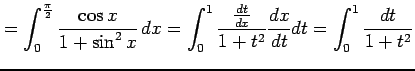 |
||
![$\displaystyle = \Big[\mathrm{Tan}^{-1} x\Big]_{0}^{1}= \mathrm{Tan}^{-1}(1)-\mathrm{Tan}^{-1}(0)= \frac{\pi}{4}-0=\frac{\pi}{4}\,.$](img2717.png) |
ここで
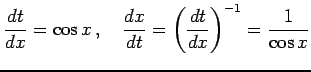 |
であることを用いた. また積分区間は
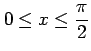 から
から
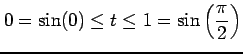 へと変わる.
へと変わる.
例 6.78 (双曲線関数を用いた定積分)
定積分
を考える. 積分区間が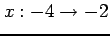 であるから
であるから 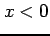 である.
このことに注意して変数変換を
である.
このことに注意して変数変換を
とする.このとき積分区間は
となる.また
であることを用いると
となる.ここで
であることを用いる.このとき
より
となる.また
である.よって
を得る.
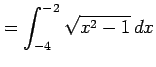 |
を考える. 積分区間が
とする.このとき積分区間は
となる.また
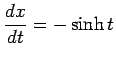 |
であることを用いると
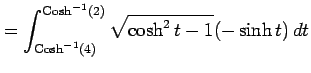 |
||
| (積分区間をひっくり返す.
|
||
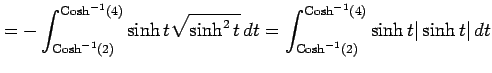 |
||
| (
|
||
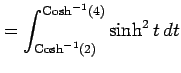 |
||
| (
|
||
![$\displaystyle = \frac{1}{2} \int^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)...
... \frac{1}{2}\sinh(2t)-t \right]^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)}$](img2740.png) |
||
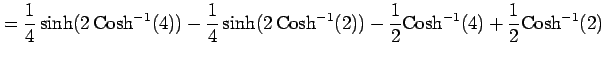 |
となる.ここで
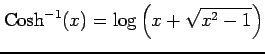 |
であることを用いる.このとき
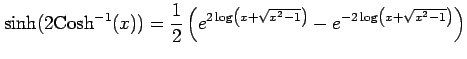 |
||
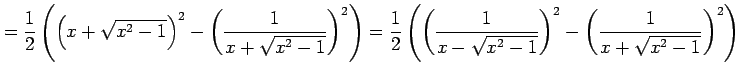 |
||
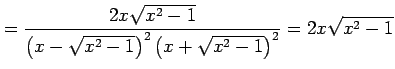 |
より
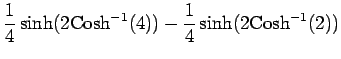 |
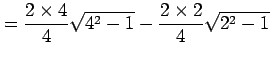 |
|
となる.また
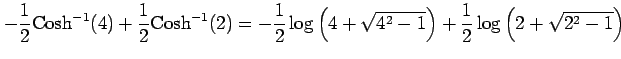 |
||
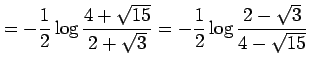 |
である.よって
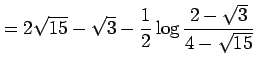 |
||
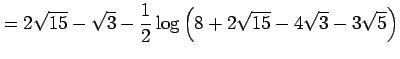 |
を得る.
例 6.79 (双曲線関数を用いた定積分)
定積分
を求める.
とおく.すると,
となる.ここで,
である.これらを代入すると
を得る.
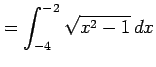 |
を求める.
とおく.すると,
![$\displaystyle = \frac{1}{4} \int_{\alpha}^{\beta}\left( t-\frac{2}{t}+\frac{1}{...
...ac{1}{4} \left[ \frac{t^2}{2}- 2\log t- \frac{1}{2t^2} \right]_{\alpha}^{\beta}$](img2754.png) |
||
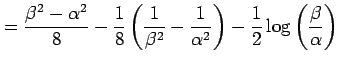 |
となる.ここで,
である.これらを代入すると
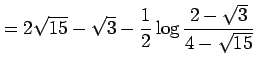 |
||
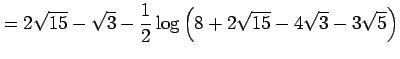 |
を得る.
平成19年10月3日