4.7 等比数列の極限
例 4.23 (等比数列の極限)
等比数列
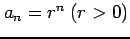 の極限を考える.
(i)
の極限を考える.
(i) 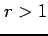 , (ii)
, (ii) 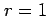 , (iii)
, (iii) 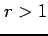 の場合に分けて議論する.
まず,(i)
の場合に分けて議論する.
まず,(i) 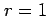 のとき,常に
のとき,常に 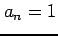 である.極限は
である.極限は 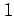 である.
つぎに,(iii)
である.
つぎに,(iii) 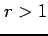 のとき,
のとき,
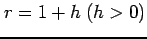 とおく.このとき
とおく.このとき 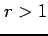 をみたす.
をみたす.
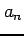 を
を 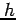 を用いて書き下すと
を用いて書き下すと
を得る.ここで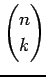 は
二項係数(binomial coefficient)であり,
は
二項係数(binomial coefficient)であり,
と定義する.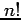 は階乗(fractorial number)であり,
は階乗(fractorial number)であり,
と再帰的に定義する.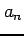 をあらためて書き直すと
をあらためて書き直すと
となる. 第三項以降を足したものは正となるので,
を得る.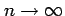 のとき
のとき
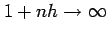 より
より
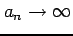 を得る.
最後に,(i)
を得る.
最後に,(i) 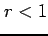 のときを考える.
のときを考える.
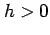 を用いて
を用いて 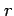 を
を
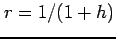 と置き換える.
このとき
と置き換える.
このとき 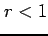 をみたす.
をみたす.
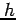 を用いて
を用いて 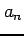 を書き下すと,
を書き下すと,
を得る. 不等式
が成立する.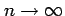 のとき
のとき
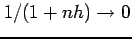 であるから,
はさみうちの定理より
であるから,
はさみうちの定理より
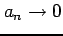 を得る.
以上をまとめると
を得る.
以上をまとめると
が求まる.
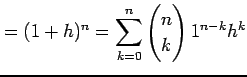 |
を得る.ここで
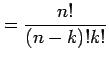 |
と定義する.
と再帰的に定義する.
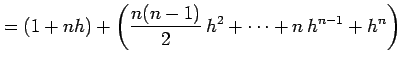 |
となる. 第三項以降を足したものは正となるので,
を得る.
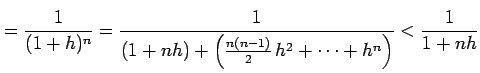 |
を得る. 不等式
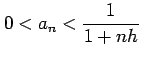 |
が成立する.
![$\displaystyle \lim_{n\to\infty} a_{n}=\lim_{n\to\infty} r^{n}= \left\{ \begin{array}{cc} 0 & (r<1)\\ [1em] 1 & (r=1)\\ [1em] \infty & (r>1) \end{array} \right.$](img1366.png) |
が求まる.
問 4.24 (極限の計算)
次の漸化式で与えられる数列の一般項と極限を求めよ.
(2)
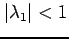 かつ
かつ
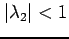 のとき
のとき 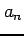 は 0
に収束する.
それ以外は発散する.
は 0
に収束する.
それ以外は発散する.
- (1)
-
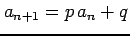 .
.
- (2)
-
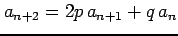 .
.
(答え) (1)
![$\displaystyle = \left\{\begin{array}{lc} \displaystyle{ p^{n-1}\left(a_{1}-\fra...
...ht)} & (p\neq1) \\ [1em] \displaystyle{(n-1)q+a_{1}} & (p=1) \end{array}\right.$](img1369.png) |
![$\displaystyle \lim_{n\to\infty}a_{n}= \left\{ \begin{array}{lc} \infty & (\vert p\vert\geq1) \\ [1em] 0 & (\vert p\vert<1) \end{array} \right.$](img1370.png) |
(2)
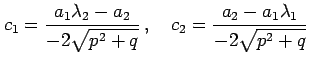 |
平成19年10月3日