2.31 ライプニッツ則
定理 2.134 (ライプニッツ則)
1 変数関数 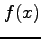 ,
, 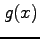 の積の
の積の 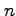 回微分は
回微分は
で与えられる. これをライプニッツ則(Leibnitz rule)という.
と表される.よって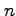 回微分は
回微分は
となる.
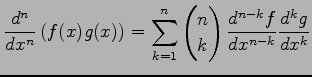 |
で与えられる. これをライプニッツ則(Leibnitz rule)という.
(証明)
積 ![]() を微分すると
を微分すると
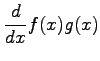 |
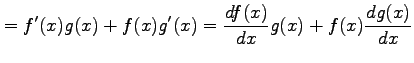 |
|
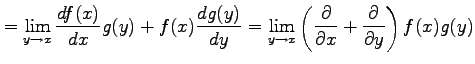 |
と表される.よって
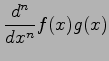 |
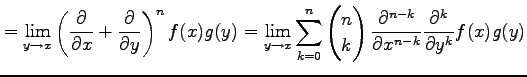 |
|
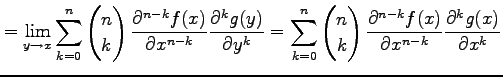 |
となる.
例 2.135 (積の微分)
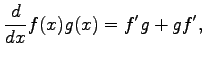 |
||
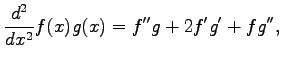 |
||
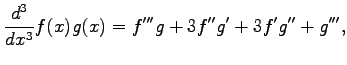 |
||
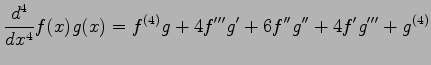 |
問 2.136 (積の微分)
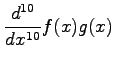 を求めよ.
を求めよ.
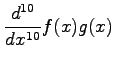 を求めよ.
を求めよ.
平成20年2月2日