3.3 2 重積分の計算
例 3.15 (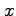 ,
, 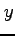 両方に単純な領域における多重積分)
領域
両方に単純な領域における多重積分)
領域  を下図のような三角形の領域とする.このとき多重積分
を下図のような三角形の領域とする.このとき多重積分
を求める. 被積分関数は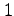 であるから,
領域
であるから,
領域  の面積を
の面積を
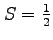 とすると,
とすると,
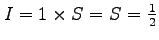 となる.
となる.
となる. このとき累次積分で計算すると
と得られる.
となる. このとき累次積分で計算すると
と得られる.
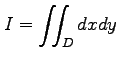 |
を求める. 被積分関数は
領域 ![]() を
を![]() に関して単純な領域として表すと
に関して単純な領域として表すと
となる. このとき累次積分で計算すると
![$\displaystyle I=\iint_{D}dxdy= \int_{0}^{1}dx\int_{0}^{x}dy= \int_{0}^{1}\left\...
...ight1.5em width0em depth0.1em\,{\frac{x^2}{2}}\,\right]_{x=0}^{x=1}=\frac{1}{2}$](img1692.png) |
と得られる.
領域 ![]() を
を ![]() に関して単純な領域として表すと
に関して単純な領域として表すと
となる. このとき累次積分で計算すると
![$\displaystyle =\iint_{D}dxdy= \int_{0}^{1}dy\int_{y}^{1}dy= \int_{0}^{1}\left\{...
...em depth0.1em\,{y-\frac{y^2}{2}}\,\right]_{y=0}^{y=1}=1-\frac{1}{2}=\frac{1}{2}$](img1695.png) |
と得られる.
注意 3.16 (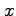 ,
, 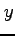 両方に単純な領域における多重積分)
両方に単純な領域における多重積分)
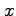 ,
, 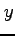 の両方に関して単純な領域であれば,
とちらの領域で計算しても結果は同じ.
の両方に関して単純な領域であれば,
とちらの領域で計算しても結果は同じ.
![\includegraphics[width=0.5\textwidth]{sekibun-D1.eps}](img1696.png) |
![\includegraphics[width=0.5\textwidth]{sekibun-I1.eps}](img1697.png) |
例 3.17 (累次積分)
多重積分
を求める. は
は 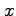 に関して単純な領域だから,
累次積分を用いて計算して,
に関して単純な領域だから,
累次積分を用いて計算して,
と得られる.
 |
を求める.
![$\displaystyle =\int_{0}^{1}dx\int_{x}^{2x}(x^2+y^2+1)dy= \int_{0}^{1}\left\{\le...
...5em width0em depth0.1em\,{x^2y+\frac{y^3}{3}+y}\,\right]_{y=x}^{y=2x}\right\}dx$](img1699.png) |
||
![$\displaystyle = \int_{0}^{1} \left\{ \left(2x^3+\frac{8x^3}{3}+2x\right)- \left...
...0em depth0.1em\,{\frac{5x^4}{6}+\frac{x^2}{2}}\,\right]_{x=0}^{x=1}=\frac{4}{3}$](img1700.png) |
と得られる.
問 3.18 (累次積分)
領域  を 2 つの
を 2 つの 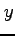 に関して単純な領域
に関して単純な領域
に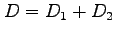 と分ける.
このとき,
と分ける.
このとき,
を計算せよ.
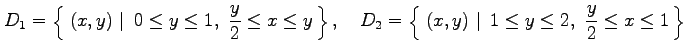 |
に
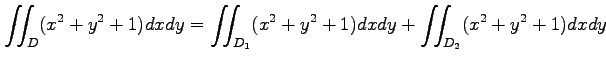 |
を計算せよ.
問 3.19 (領域の面積)
領域  の面積
の面積
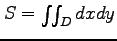 を求めよ.
を求めよ.
![\includegraphics[width=0.35\textwidth]{sekibun-D2.eps}](img1706.png) |
![\includegraphics[width=0.35\textwidth]{sekibun-D2y.eps}](img1707.png) |
![\includegraphics[width=0.35\textwidth]{sekibun-I2.eps}](img1708.png) |
| (a) |
(b) |
(c) |
例 3.20 (累次積分)
多重積分
を求める. は
は 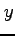 に関して単純な領域だから,
累次積分を用いて計算して,
に関して単純な領域だから,
累次積分を用いて計算して,
と得られる.
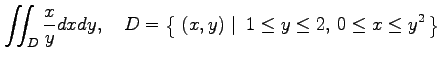 |
を求める.
![$\displaystyle =\int_{1}^{2}dy\int_{0}^{y^2}\frac{x}{y}dx= \int_{1}^{2}\left\{\l...
...ht1.5em width0em depth0.1em\,{\frac{y^4}{8}}\,\right]_{y=1}^{y=2}= \frac{15}{8}$](img1710.png) |
と得られる.
問 3.21 (累次積分)
領域  を 2 つの
を 2 つの 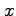 に関して単純な領域
に関して単純な領域
に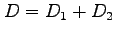 と分ける.
このとき,
と分ける.
このとき,
を計算せよ.
に
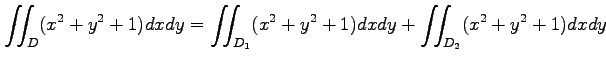 |
を計算せよ.
問 3.22 (領域の面積)
領域  の面積
の面積
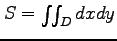 を求めよ.
を求めよ.
![\includegraphics[width=0.35\textwidth]{sekibun-D3.eps}](img1712.png) |
![\includegraphics[width=0.35\textwidth]{sekibun-D3x.eps}](img1713.png) |
![\includegraphics[width=0.4\textwidth]{sekibun-I3.eps}](img1714.png) |
| (a) |
(b) |
(c) |
例 3.23 (累次積分)
多重積分
を求める.領域 は半円の内部の領域であり,
は半円の内部の領域であり,
と書き直すと,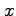 に関して単純な領域とする.
累次積分を用いて計算して,
に関して単純な領域とする.
累次積分を用いて計算して,
と得られる.
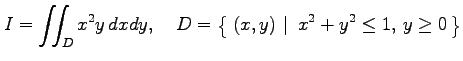 |
を求める.領域
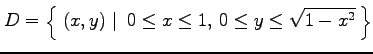 |
と書き直すと,
![$\displaystyle =\int_{0}^{1}dx\int_{0}^{\sqrt{1-x^2}}\!\!\!\!\!\!\!\!\!\!\!x^2y\...
...t1.5em width0em depth0.1em\,{\frac{x^3}{6}-\frac{x^5}{10}}\,\right]_{x=0}^{x=1}$](img1717.png) |
||
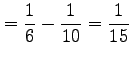 |
と得られる.
問 3.24 (累次積分)
領域  を
を 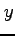 に関して単純な領域として書けば
に関して単純な領域として書けば
と書ける.このとき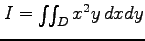 を求めよ.
を求めよ.
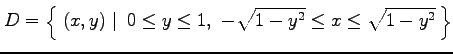 |
と書ける.このとき
問 3.25 (領域の面積)
領域  の面積
の面積
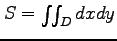 を求めよ.
を求めよ.
![\includegraphics[width=0.5\textwidth]{sekibun-D4.eps}](img1721.png) |
![\includegraphics[width=0.5\textwidth]{sekibun-D4y.eps}](img1722.png) |
| (a) |
(b) |
平成20年2月2日