3.8 多重積分の置換積分
注意 3.44 (定積分の置換積分)
定積分において積分変数を 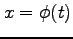 と置き換えると
と置き換えると
となる. ただし,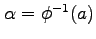 ,
,
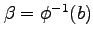 である.
である.
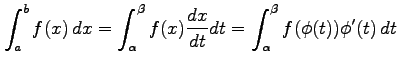 |
となる. ただし,
定理 3.45 (多重積分の置換積分)
多重積分
において積分変数を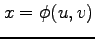 ,
,
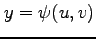 と置き換える.
このとき,
と置き換える.
このとき,
となる.ただし,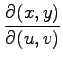 は
ヤコビアン
は
ヤコビアン
であり,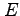 は
は 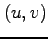 の領域
の領域
である.
と表される.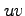 座標に座標変換すると,
座標に座標変換すると,
とおける. このとき,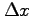 ,
, 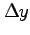 は十分小さいとすると,
は十分小さいとすると,
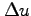 ,
, 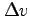 も十分小さいので,
テイラー展開して
も十分小さいので,
テイラー展開して
と書ける.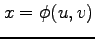 ,
,
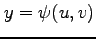 であることに注意すると
であることに注意すると
が成り立つ. ここで,ベクトル
は点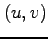 における
における 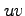 座標の基底となる.
座標の基底となる.
となる. 極限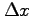 ,
,
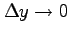 においてもこれが成り立つので,
においてもこれが成り立つので,
を得る.
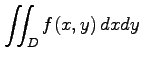 |
において積分変数を
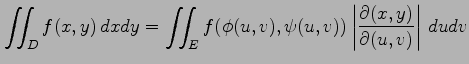 |
となる.ただし,
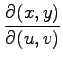 は
ヤコビアン
は
ヤコビアン
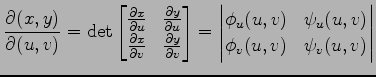 |
であり,
である.
(証明)
![]() 座標の点
座標の点 ![]() ,
,
![]() は
標準基底
は
標準基底 ![]() ,
, ![]() を用いて,
を用いて,
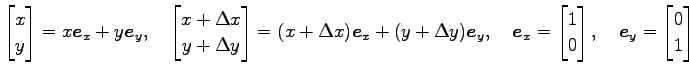 |
と表される.
とおける. このとき,
と書ける.
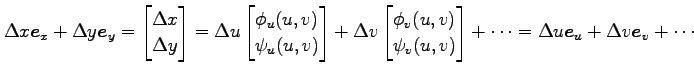 |
が成り立つ. ここで,ベクトル
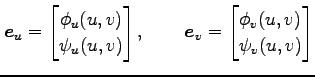 |
は点
頂点が ![]() ,
,
![]() ,
,
![]() ,
,
![]() からなる長方形の微小領域の面積は
からなる長方形の微小領域の面積は
![]() である.
一方,
である.
一方,![]() 座標において頂点が
座標において頂点が
![]() ,
,
![]() ,
,
![]() ,
,
![]() からなる領域は平行四辺形である.
平行四辺形
からなる領域は平行四辺形である.
平行四辺形 ![]() の面積は,
の面積は,
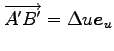 ,
,
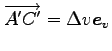 より,
より,
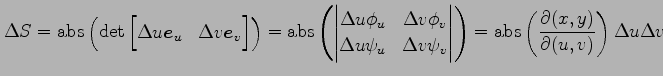 |
となる. 極限
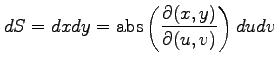 |
を得る.
注意 3.46 (置換積分)
1 変数関数の定積分では
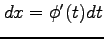 に絶対値はつかない.
これは積分区間
に絶対値はつかない.
これは積分区間 ![$ [a,b]$](img1633.png) に向きを考えているためである.
例えば,
に向きを考えているためである.
例えば,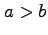 のとき定積分の値の符合は反転される.
多重積分では,
のとき定積分の値の符合は反転される.
多重積分では,
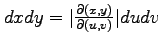 に
絶対値がつく.
これは面積要素に向きを考えないためである.
に
絶対値がつく.
これは面積要素に向きを考えないためである.
![\includegraphics[width=0.5\textwidth]{chikan-th-xy.eps}](img1842.png) |
![\includegraphics[width=0.4\textwidth]{chikan-th-uv.eps}](img1843.png) |
| (a) |
(b) |
平成20年2月2日