1.5 演習問題 〜 変数分離型,同次型,完全微分型
問 1.15 (変数分離型)
次の変数分離型方程式の一般解を求め解曲線を図示せよ.
また,初期条件 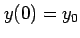 のときの特殊解もそれぞれ求めよ.
のときの特殊解もそれぞれ求めよ.
(1)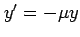 (2)
(2)
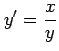 (3)
(3) 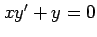 (4)
(4)
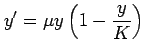
(5)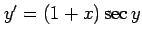 (6)
(6)
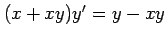 (7)
(7)
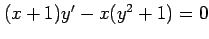
(8)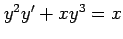 (9)
(9)
 (10)
(10) 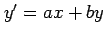 (
(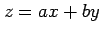 とおく)
とおく)
(11)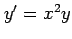 (12)
(12) 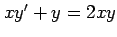 (13)
(13)
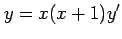 (14)
(14)
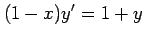
(15)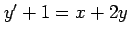 (
(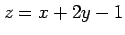 とおく)
(16)
とおく)
(16)
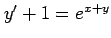 (
(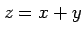 とおく)
とおく)
(17)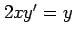 (18)
(18) 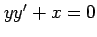 (19)
(19) 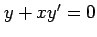 (20)
(20) 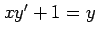
(21)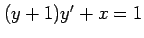 (22)
(22) 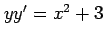 (23)
(23)
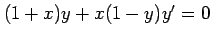
(24)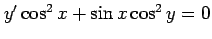 (25)
(25)
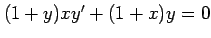 (26)
(26)

(27)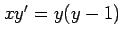 (28)
(28) 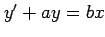 (変数変換要)
(29)
(変数変換要)
(29) 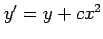 (変数変換要)
(変数変換要)
(1)
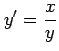 (3)
(3) 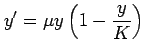
(5)
(8)
(11)
(15)
(17)
(21)
(24)
(27)
問 1.16 (同次型)
次の同次型方程式の一般解を求めよ.
また,初期値 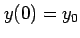 における特殊解を求めよ.
さらには,解曲線を図示せよ.
における特殊解を求めよ.
さらには,解曲線を図示せよ.
(1)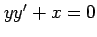 (2)
(2)
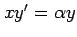 (3)
(3)
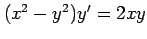 (4)
(4)
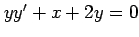
(5)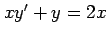 (6)
(6)
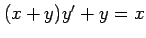 (7)
(7)
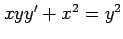 (8)
(8)
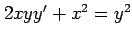
(9)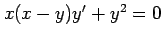 (10)
(10)
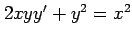 (11)
(11) 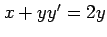 (12)
(12)
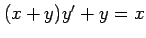
(13)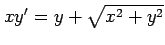 (14)
(14)
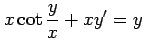 (15)
(15)
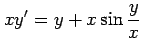
(16)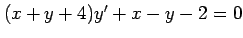 (17)
(17) 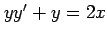 (18)
(18)
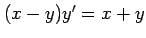
(1)
(5)
(9)
(13)
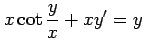 (15)
(15)
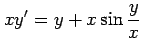
(16)
問 1.17 (完全微分型)
次の方程式の一般解を求めよ.
(1)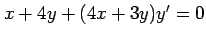 (2)
(2)
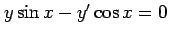 (3)
(3)
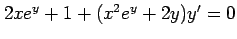
(4)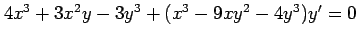 (5)
(5)
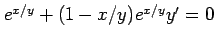
(6)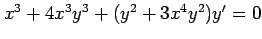 (7)
(7)
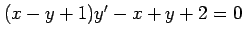
(8)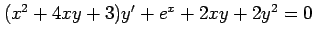 (9)
(9)
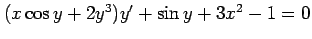
(10)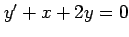 (11)
(11)
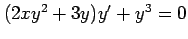 (12)
(12)
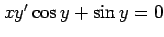
(13)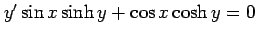 (14)
(14)
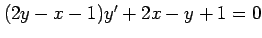
(15)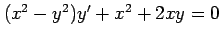 (16)
(16)
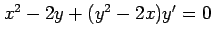
(17)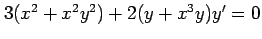 (18)
(18)
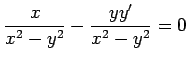
(1)
(4)
(6)
(8)
(10)
(13)
(15)
(17)
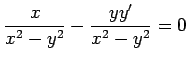
問 1.18 (完全微分型)
次の方程式の積分因子を求め一般解を求めよ.
(1)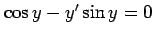 (2)
(2)
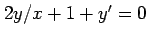 (3)
(3)
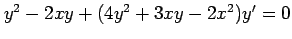
(4)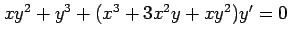 (5)
(5) 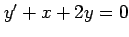 (6)
(6)
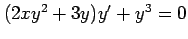
(7)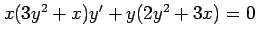 (8)
(8) 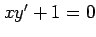 (9)
(9)
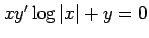
(10)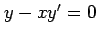 (11)
(11) 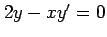 (12)
(12)
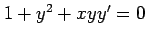 (13)
(13)
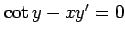
(1)
(4)
(7)
(10)
問 1.19 (直交曲線族)
次の曲線族の直交曲線族を求め図示せよ.
(1)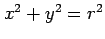 (2)
(2)
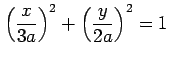 (3)
(3)
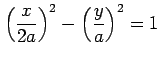
(4)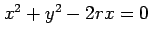
(1)
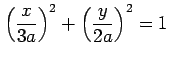 (3)
(3)
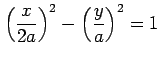
(4)
注意 1.20 (三角関数の逆数)
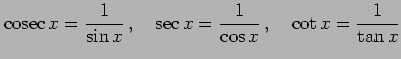 |
平成19年4月9日