6.7 有理関数の積分
有理関数
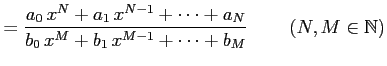 |
の不定積分
 |
を考える. 任意の有理関数は積分可能である.
Step 1 (分子を分母で割る)
分子の次数 ![]() が分母の次数
が分母の次数 ![]() 以上のときは
まず割り算を行い,
以上のときは
まず割り算を行い,
 |
とする. このとき多項式の部分は必ず積分が可能である. よって以後では分子の次数
Step 2 (分母を因数分解する)
有理式を
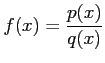 とする.
分母の多項式
とする.
分母の多項式 ![]() を実数の範囲で因数分解する.
このとき
を実数の範囲で因数分解する.
このとき
と表される.
Step 3 (部分分数分解する)
有理式
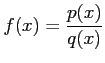 を
部分分数分解する.
すなわち
を
部分分数分解する.
すなわち
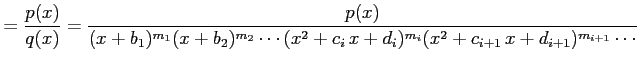 |
||
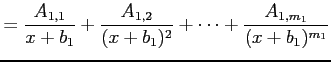 |
||
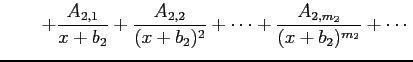 |
||
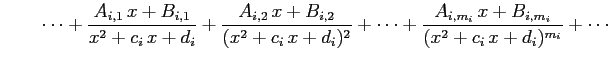 |
と変形する.
問 6.41 (部分分数分解)
任意の有理式
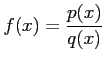
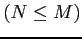 は
上式のように部分分数分解される.これを示せ.
は
上式のように部分分数分解される.これを示せ.
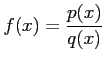
Step 4 (部分分数ごとに積分する)
部分分数ごとに積分を行う.
すなわち
 |
||
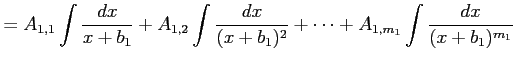 |
||
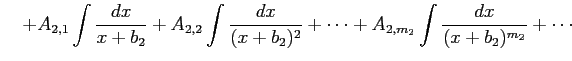 |
||
 |
を計算する. それぞれの場合ごとに積分を考える.
分母の因子が ![]() 次式の場合
次式の場合
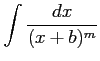 |
の積分を行なう.
Type 1: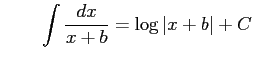 |
となる.
Type 2: |
となる.
分母の因子が ![]() 次式の場合の積分を行なう.
次式の場合の積分を行なう.
![]() 次式の判別式が負であることに注意すると
次式の判別式が負であることに注意すると
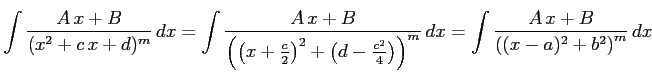 |
||
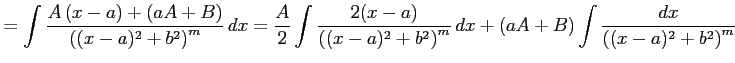 |
||
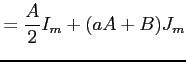 |
と表される. ここで
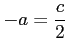 ,
,
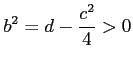 ,
, 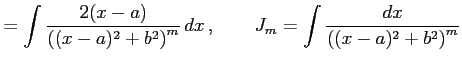 |
とおいた. 積分
| Type 3: |
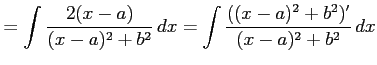 |
|
となり,
| Type 4: |
 |
|
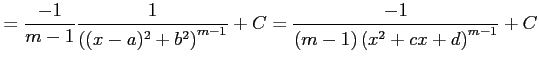 |
と求まる. 第二項目の積分
| Type 5: |
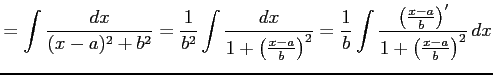 |
|
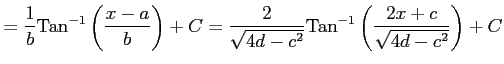 |
となる.
| Type 6: |
 |
|
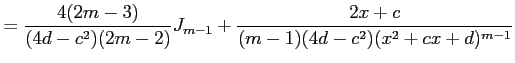 |
より
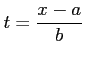 とおいて置換積分を用いると
とおいて置換積分を用いると
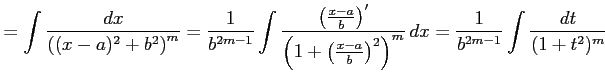 |
となる. 分子を変形すると
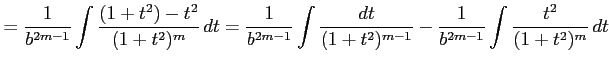 |
第 1 項は
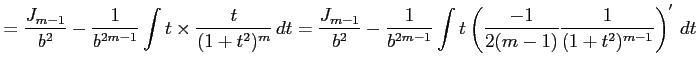 |
||
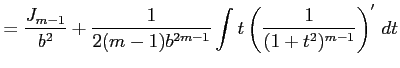 |
||
 |
となる.残った積分も
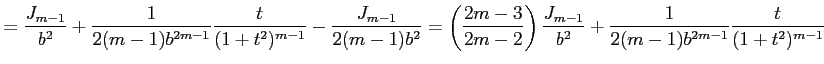 |
||
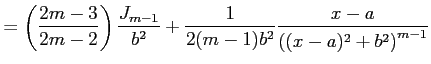 |
となり漸化式を得る.
平成21年6月1日