6.9 有理関数の積分 〜 分母の因数分解
定義 6.43 (多項式の根)
多項式
に対して,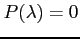 をみたすとき,
をみたすとき,
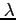 を多項式
を多項式 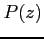 の
根(root)という.
の
根(root)という.
に対して,
定義 6.44 (重根)
ある複数の根が同じ値となるとき,
それらの根を重根(multiple root)と呼ぶ.
定理 6.45 (多項式の根)
重根を別の根とみなすとき,
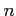 次多項式は
次多項式は 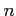 個の根をもつ.
個の根をもつ.
定理 6.46 (因数分解)
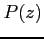 の
の 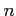 個の根が
個の根が 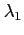 ,
, 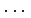 ,
, 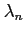 のとき
のとき
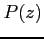 は
は
と因数分解される.
と因数分解される.
定理 6.47 (実係数多項式の虚根)
実係数の多項式 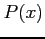 ,
,
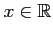 ,
,
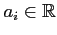 が
ある虚数根
が
ある虚数根 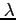 をもつとき,
その複素共役
をもつとき,
その複素共役
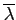 も根となる.
も根となる.
が成り立つ.
(証明)
![]() とする.このとき,
とする.このとき,
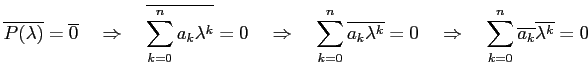 |
||
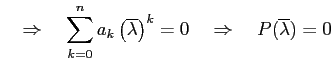 |
が成り立つ.
定理 6.48 (実係数の多項式の因数分解)
実係数の多項式 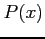 ,
,
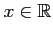 ,
,
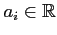 を
実数の範囲内で因数分解すると,
1 次多項式と判別式が負の 2 次多項式で因数分解される.
を
実数の範囲内で因数分解すると,
1 次多項式と判別式が負の 2 次多項式で因数分解される.
とすると実係数となる. この 2 次多項式の判別式は
であり負となる. ただし,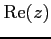 ,
,
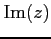 は
それぞれ複素数
は
それぞれ複素数 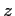 の実部,虚部を表し,
の実部,虚部を表し,
と表される.
(証明)
根 ![]() が実数のときは因子を
が実数のときは因子を ![]() とする.
根
とする.
根 ![]() が虚数のときは,
その複素共役
が虚数のときは,
その複素共役
![]() も根となるので,
も根となるので,
とすると実係数となる. この 2 次多項式の判別式は
であり負となる. ただし,
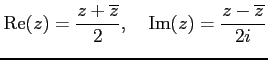 |
と表される.
例 6.49 (複素数の範囲内で因数分解)
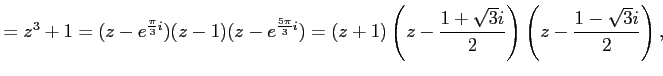 |
||
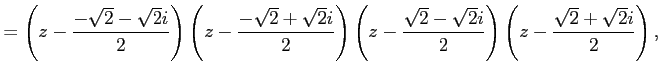 |
||
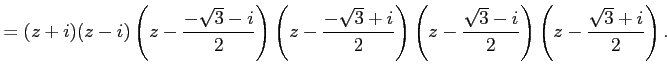 |
注意 6.50 (因数分解)
奇数次の多項式は必ず一つは実根をもつ.
例 6.51 (実数の範囲内で因数分解)
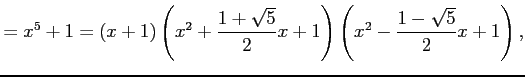 |
||
例 6.52 (分母の因数分解)
平成21年6月1日