6.26 パラメータで表される曲線の長さ
定理 6.126 (曲線の長さ)
曲線 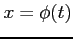 ,
, 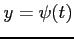 ,
,
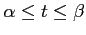 の長さは
の長さは
により得られる.
となる.
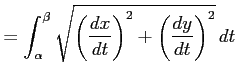 |
により得られる.
(証明)
![]() ,
,
![]() として,
置換積分すると
として,
置換積分すると
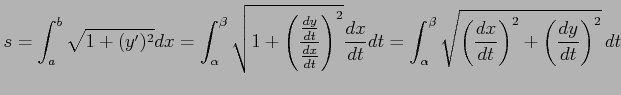 |
となる.
例 6.127 (サイクロイド)
サイクロイド
の曲線の長さ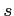 と,
サイクロイドと
と,
サイクロイドと 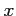 軸とで囲まれた領域の面積
軸とで囲まれた領域の面積 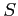 を求める.
を求める.
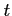 の積分区間は
の積分区間は ![$ [0,2\pi]$](img3488.png) であり,
であり,
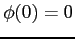 ,
,
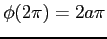 より
より
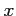 の積分区間は
の積分区間は ![$ [0,2a\pi]$](img3491.png) であることに注意して積分すると,
であることに注意して積分すると,
の曲線の長さ
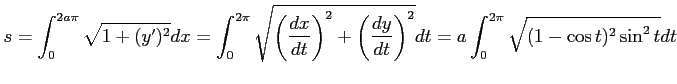 |
||
![$\displaystyle = a\int_{0}^{2\pi}\sqrt{2(1-\cos t)}dt= a\int_{0}^{2\pi}\sqrt{4\s...
...ule height1.5em width0em depth0.1em\,{-\cos\frac{t}{2}}\,\right]_{0}^{2\pi}=8a,$](img3493.png) |
||
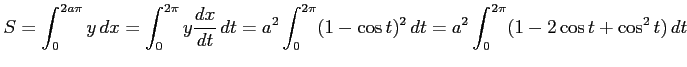 |
||
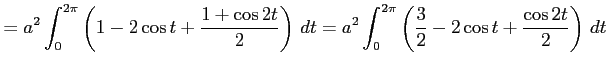 |
||
![$\displaystyle = a^2\left[\vrule height1.5em width0em depth0.1em\,{\frac{3}{2}t-2\sin t+\frac{1}{4}\sin 2t}\,\right]_{0}^{2\pi}= 3\pi a^2\,.$](img3496.png) |
平成21年6月1日