3.21 演習 〜 高階導関数
問 3.66 (高階導関数)
次の関数の高階導関数を求めよ.
(1)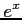 (2)
(2)
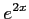 (3)
(3)
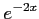 (4)
(4)
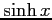 (5)
(5)
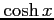 (6)
(6)
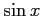 (7)
(7)
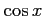 (8)
(8)
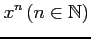
(9)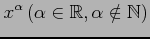 (10)
(10)
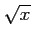 (11)
(11)
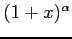 (
(
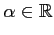 ,
,
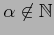 )
(12)
)
(12)
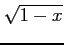 (13)
(13)
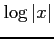
(14)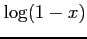
(1)
(9)
(14)
問 3.67 (高階導関数)
次の関数の 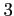 階までの導関数を求めそのグラフを描け.
階までの導関数を求めそのグラフを描け.
(1)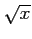 (2)
(2)
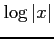 (3)
(3) 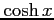
(1)
問 3.68 (なめらかさ)
次の関数は
不連続関数,
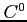 級関数,
級関数,
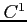 級関数,
級関数,
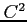 級関数,
級関数,
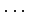 ,
,
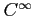 級関数のうちどれか答えよ.
(ヒント:すべての高階導関数を求めグラフを描く.)
級関数のうちどれか答えよ.
(ヒント:すべての高階導関数を求めグラフを描く.)
(1)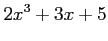 (2)
(2)
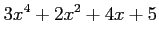 (3)
(3) 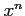 (4)
(4) 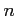 次多項式
(5)
次多項式
(5) 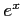
(6)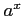 (
(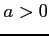 )
(7)
)
(7) 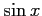 (8)
(8) 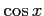 (9)
(9)
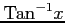 (10)
(10)
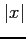 (11)
(11)
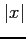 (12)
(12)
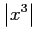
(13)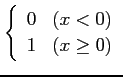 (14)
(14)
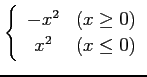 (15)
(15)
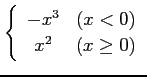 (16)
(16)
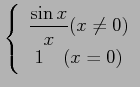
(1)
(6)
(13)
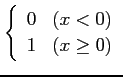 (14)
(14)
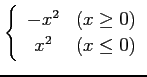 (15)
(15)
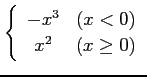 (16)
(16)
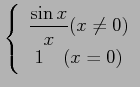
問 3.69 (ライブニッツ則)
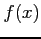 ,
,
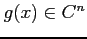 に対して次の関係式が成立することを示せ.
に対して次の関係式が成立することを示せ.
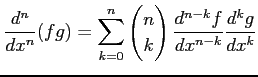 |
問 3.70 (ライプニッツ則)
次の関数の高階導関数をライプニッツ則を用いて求めよ.
(1)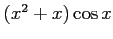 (2)
(2)
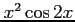 (3)
(3) 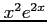 (4)
(4)
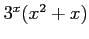 (5)
(5)
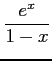 (6)
(6)
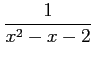
(1)
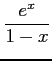 (6)
(6)
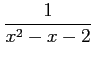
問 3.71 (合成関数の高階導関数)
次の関係式が成立すること示せ.
(1)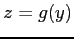 ,
, 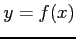 に対して
に対して
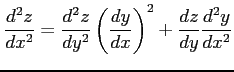
(2)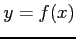 ,
,
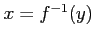 に対して
に対して
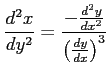
(1)
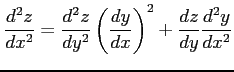
(2)
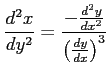
問 3.72 (凹凸,変曲点)
次の関数の増減,極値,凹凸,変曲点を調べグラフを描け.
(1)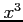 (2)
(2)
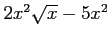 (3)
(3)
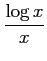
(1)
問 3.73 (高階導関数)
次の表の空いている個所を埋めよ.
|
|
|
|
|
|
|
|
0 | 0 | 0 | 0 |
|
|
|
|
|
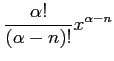 (
(
|
|
(
|
0 (
|
|||
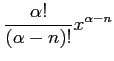 (
(
|
||||
|
|
|
|||
|
|
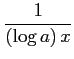 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
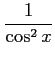 |
|||
|
|
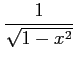 |
|||
|
|
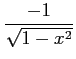 |
|||
|
|
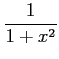 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
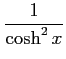 |
|||
|
|
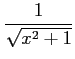 |
|||
|
|
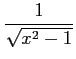 |
|||
|
|
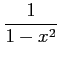 |
平成21年6月1日