2.14 全微分可能性と偏微分可能性
定理 2.66 (全微分可能の必要条件)
関数 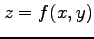 が全微分可能であれば,
が全微分可能であれば,
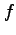 は偏微分可能であり,
は偏微分可能であり,
が成り立つ.
が成り立つ. 軸に沿って極限をとる.
軸に沿って極限をとる.
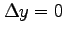 ,
,
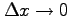 とする.
このとき,
とする.
このとき,
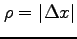 であるから,
であるから,
が成り立つ. これは
と等価である. また,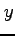 軸に沿って極限をとる.
軸に沿って極限をとる.
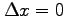 ,
,
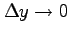 とすると,
同様にして
とすると,
同様にして
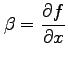 を得る.
を得る.
 |
が成り立つ.
(証明)
関数 ![]() が全微分可能であれば,
が全微分可能であれば,
が成り立つ.
が成り立つ. これは
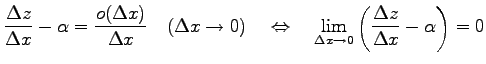 |
||
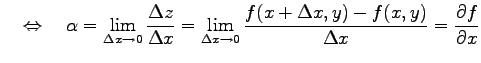 |
と等価である. また,
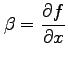 を得る.
を得る.
平成21年1月14日