2.24 演習問題 〜 合成関数の微分
問 2.99 (合成関数の微分)
次の合成関数の導関数
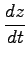 を求めよ.
を求めよ.
(1)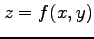 ,
,
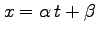 ,
,
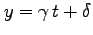 (2)
(2) 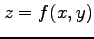 ,
,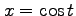 ,
,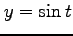
(3) ,
,
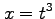 ,
,
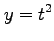 (4)
(4)
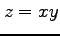 ,
,
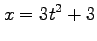 ,
,
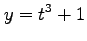
(5)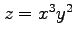 ,
,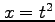 ,
,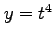 (6)
(6)
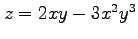 ,
,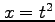 ,
,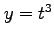
(7)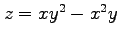 ,
,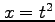 ,
,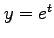 (8)
(8)
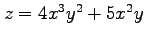 ,
,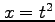 ,
,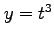
(9)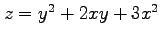 ,
, 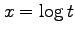 ,
, 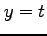 (10)
(10)
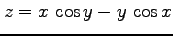 ,
,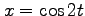 ,
,
(11)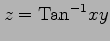 ,
,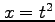 ,
,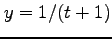 (12)
(12)
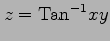 ,
,
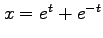 ,
,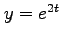
(13)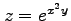 ,
,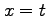 ,
,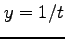 (14)
(14)
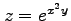 ,
,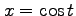 ,
,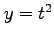
(15)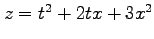 ,
,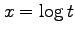 (16)
(16)
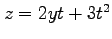 ,
, 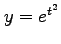
(1)
(3)
(5)
(7)
(9)
(11)
(13)
(15)
問 2.100 (合成関数の微分)
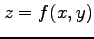 に対して,
次の高階導関数を求めよ.
に対して,
次の高階導関数を求めよ.
(1)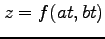 のとき,
のとき,
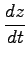 ,
,
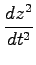 ,
,
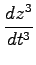 ,
,
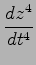 を求めよ.
を求めよ.
(2)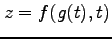 のとき,
のとき,
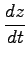 ,
,
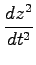 を求めよ.
を求めよ.
(3)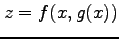 のとき,
のとき,
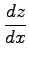 ,
,
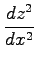 を求めよ.
を求めよ.
(1)
(2)
(3)
問 2.101 (合成関数の微分)
次の合成関数の偏導関数
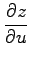 ,
,
 を求めよ.
を求めよ.
(1)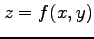 ,
,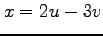 ,
,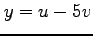 (2)
(2) 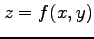 ,
,
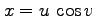 ,
,
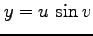
(3)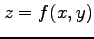 ,
,
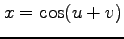 ,
,
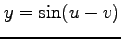 (4)
(4) 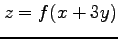 ,
,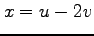 ,
,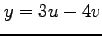
(5)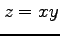 ,
,
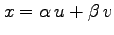 ,
,
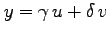 (6)
(6)
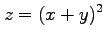 ,
,
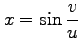 ,
,
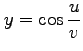
(7)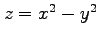 ,
,
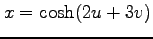 ,
,
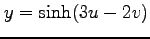
(8)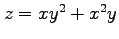 ,
,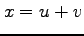 ,
,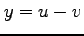 (9)
(9)
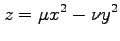 ,
,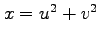 ,
,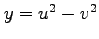
(10)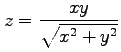 ,
,
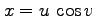 ,
,
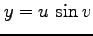 (11)
(11)
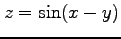 ,
,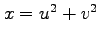 ,
,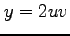
(12)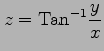 ,
,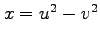 ,
,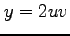 (13)
(13)
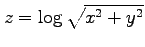 ,
,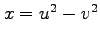 ,
,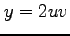
(1)
(3)
(5)
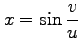 ,
,
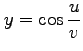
(7)
(8)
(10)
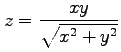 ,
,
(12)
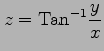 ,
,
問 2.102 (合成関数の微分)
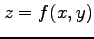 ,
, 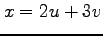 ,
, 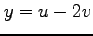 のとき,次を示せ.
のとき,次を示せ.
(1)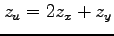 ,
,
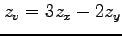 (2)
(2)
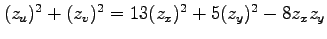
(1)
問 2.103 (合成関数の微分)
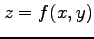 ,
,
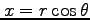 ,
,
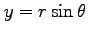 のとき,次を示せ.
のとき,次を示せ.
(1)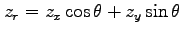 ,
,
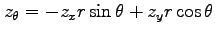 (2)
(2)
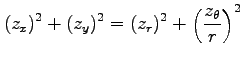
(1)
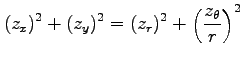
問 2.104 (合成関数の微分)
次の関数 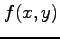 の点
の点 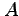 における
方向
における
方向 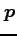 の方向微分を求めよ.
の方向微分を求めよ.
(1)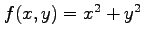 ,
, 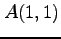 ,
,
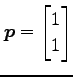 (2)
(2) 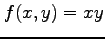 ,
, 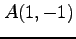 ,
,
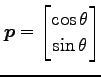
(1)
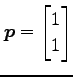 (2)
(2) 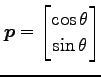
平成21年1月14日