2.29 斜交座標
![]() 次元ユークリッド空間に
普通に導入する座標
次元ユークリッド空間に
普通に導入する座標 ![]() は,
標準基底
は,
標準基底
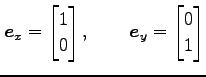 |
における座標である. 座標を
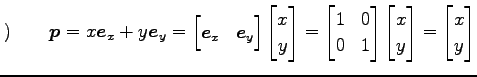 |
と表される. 一方, 基底
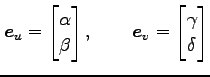 |
における座標を
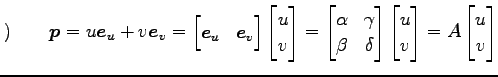 |
と表される. ベクトル
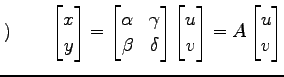 |
が成り立つ.
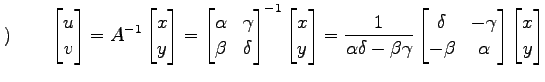 |
が成り立つ. (○)を座標
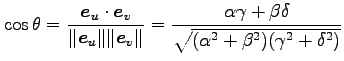 |
は一般には 0 とはならないので, 座標
例 2.117 (斜交座標における偏導関数)
直交座標  から斜交座標
から斜交座標 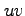 への座標変換(○)を考える.
関数
への座標変換(○)を考える.
関数  における
における 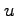 ,
, 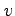 に関する偏導関数を求める.
(○)より
に関する偏導関数を求める.
(○)より
であるから,
となり, 導関数の微分則を用いると
を得る.この関係式は
とも表される.また, ナブラ作用素
を導入すれば
と簡潔に表される.
であるから,
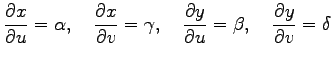 |
となり, 導関数の微分則を用いると
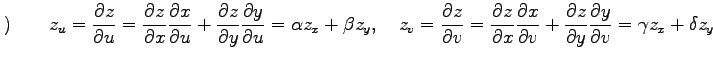 |
を得る.この関係式は
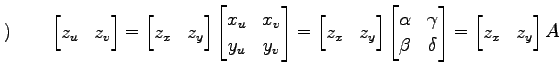 |
とも表される.また, ナブラ作用素
 |
を導入すれば
と簡潔に表される.
例 2.118 (直交座標から斜交座標へのヤコビアン)
直交座標  から斜交座標
から斜交座標 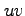 への座標変換(○)の
ヤコビアンを求める.
(♭)よりヤコビアンは
への座標変換(○)の
ヤコビアンを求める.
(♭)よりヤコビアンは
と得られる.
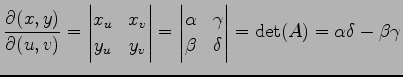 |
と得られる.
例 2.119 (斜交座標における偏微分作用素)
斜交座標 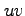 から直交座標
から直交座標 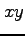 への座標変換(●)の
偏微分作用素の変換式を求める.
座標変換(○)より導出された(△)を書き直すと
への座標変換(●)の
偏微分作用素の変換式を求める.
座標変換(○)より導出された(△)を書き直すと
と書ける. 関数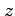 は任意でもよいので
関数を省略すると,
偏微分演算子の関係式
は任意でもよいので
関数を省略すると,
偏微分演算子の関係式
を得る. この関係式は偏微分作用素に関する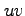 座標から
座標から 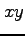 座標への変換を表す.
点に関する座標変換(○)の逆向きの変換であることに注意する.
座標への変換を表す.
点に関する座標変換(○)の逆向きの変換であることに注意する.
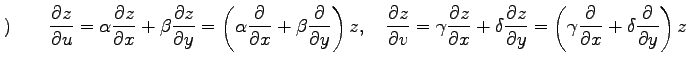 |
と書ける. 関数
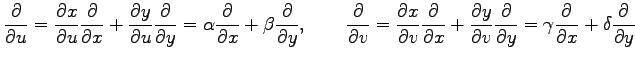 |
を得る. この関係式は偏微分作用素に関する
例 2.120 (斜交座標における偏微分作用素)
直交座標 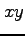 から斜交座標
から斜交座標 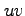 への座標変換(○)を考える.
関数
への座標変換(○)を考える.
関数 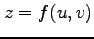 における
における  ,
, 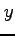 に関する偏導関数を求める.
(●)より座標変換は
に関する偏導関数を求める.
(●)より座標変換は
であるか,導関数の微分則を用いると
を得る.この関係式は
とも表される. この結果は(♭)の両辺に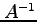 を右から
掛けることでも得られる.
また,ナブラ作用素を導入すると
を右から
掛けることでも得られる.
また,ナブラ作用素を導入すると
と簡潔に表される. 次に(▲)において関数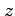 は任意で成り立つので
省略すると,
偏微分作用素の関係式
は任意で成り立つので
省略すると,
偏微分作用素の関係式
を得る. この関係式は偏微分作用素に関する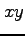 座標から
座標から 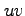 座標への変換を表す.
点に関する座標変換(●)の逆向きの変換であることに注意する.
座標への変換を表す.
点に関する座標変換(●)の逆向きの変換であることに注意する.
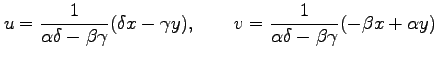 |
であるか,導関数の微分則を用いると
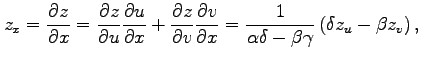 |
||
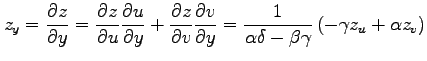 |
を得る.この関係式は
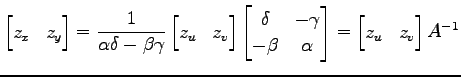 |
とも表される. この結果は(♭)の両辺に
と簡潔に表される. 次に(▲)において関数
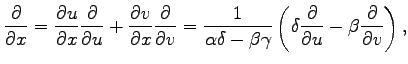 |
||
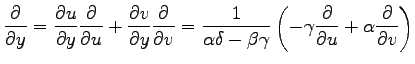 |
を得る. この関係式は偏微分作用素に関する
例 2.121 (斜交座標への座標変換)
関数 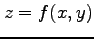 に対して関数
に対して関数
を考える. この関数を斜交座標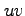 で表す.
(▲)を代入すると
で表す.
(▲)を代入すると
を得る.
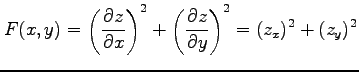 |
を考える. この関数を斜交座標
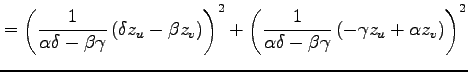 |
||
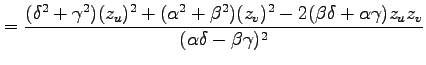 |
||
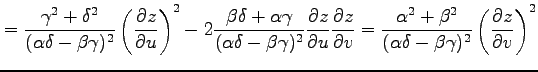 |
を得る.
例 2.122 (斜交座標におけるラプラシアン)
関数 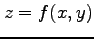 に対して関数
に対して関数
を考える. この関数を斜交座標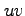 で表す.
(◎)より
で表す.
(◎)より
となるから,
を得る.
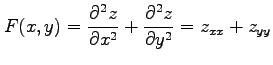 |
を考える. この関数を斜交座標
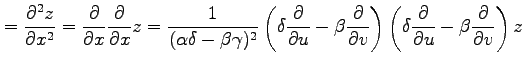 |
||
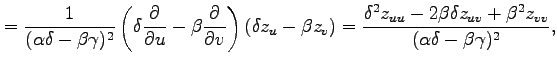 |
||
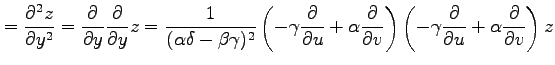 |
||
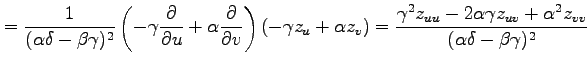 |
となるから,
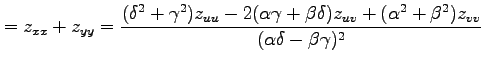 |
||
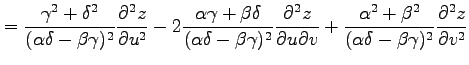 |
を得る.
例 2.123 (斜交座標におけるラプラシアン)
直交座標 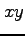 から斜交座標
から斜交座標 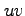 への座標変換(○)を考える.
このとき
ラプラシアン(Laplacian)または
ラプラス作用素(Laplace operator)
と呼ばれる
偏微分作用素
への座標変換(○)を考える.
このとき
ラプラシアン(Laplacian)または
ラプラス作用素(Laplace operator)
と呼ばれる
偏微分作用素
の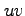 座標への変換を行う.
前例題において関数
座標への変換を行う.
前例題において関数 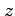 は任意であるから,
は任意であるから,
を得る.
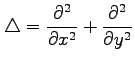 |
の
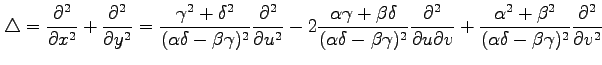 |
を得る.
平成21年1月14日