2.34 テイラー展開
1 変数関数 ![]() のテイラー展開は,点
のテイラー展開は,点 ![]() のまわりで
のまわりで ![]() について
展開すると
について
展開すると
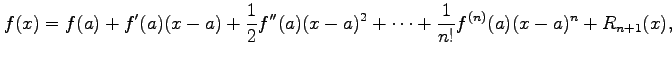 |
||
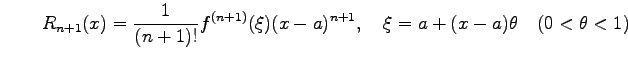 |
である.
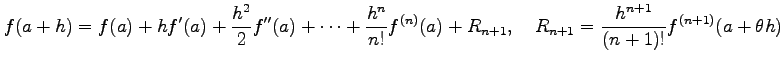 |
となる.
2 変数関数 ![]() のテイラー展開では,
点
のテイラー展開では,
点 ![]() のまわりで点
のまわりで点
![]() についての
展開を考える.
まず,関数
についての
展開を考える.
まず,関数
を導入する.これを
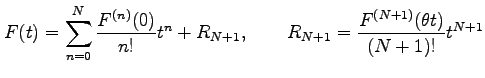 |
となる.微係数を求める.
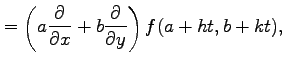 |
||
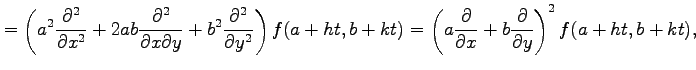 |
||
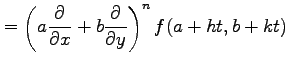 |
であるから,
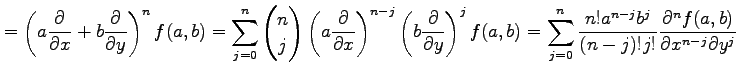 |
||
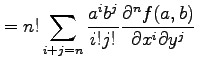 |
を得る.これを用いると,
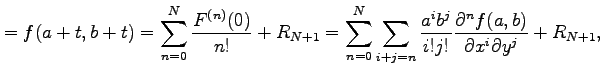 |
||
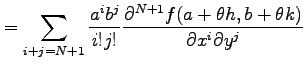 |
を得る.
定理 2.148 (テイラー展開)
関数 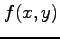 が
が 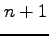 回微分可能なとき,
点
回微分可能なとき,
点 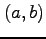 のまわりで点
のまわりで点
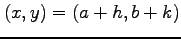 についての
テイラー展開(Taylor expansion)は,
についての
テイラー展開(Taylor expansion)は,
である与えられる.ただし,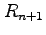 は
剰余項(remainder)であり,
は
剰余項(remainder)であり,
と与えられる.ただし,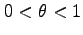 である.
である.
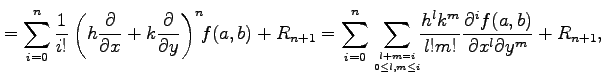 |
||
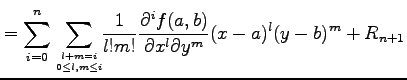 |
である与えられる.ただし,
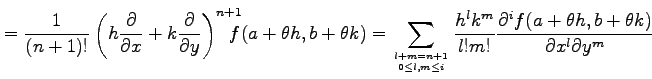 |
と与えられる.ただし,
注意 2.149 (テイラー展開)
テイラー展開をベクトル表記すると
と書ける.ただし,
であり,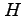 は
は 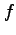 のヘッセ行列(Hesse matrix)という.
のヘッセ行列(Hesse matrix)という.
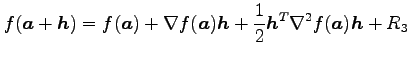 |
と書ける.ただし,
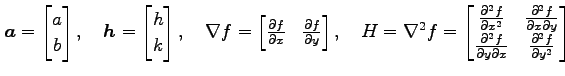 |
であり,
例 2.150 (テイラー展開)
関数 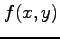 を点
を点 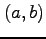 のまわりで点
のまわりで点 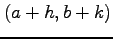 について
について
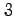 次まで展開し,
次まで展開し, 次以降を剰余項で表すと
次以降を剰余項で表すと
となる.
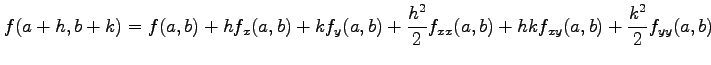 |
||
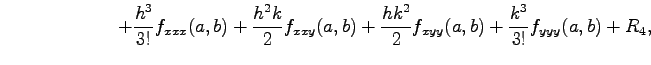 |
||
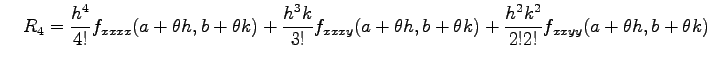 |
||
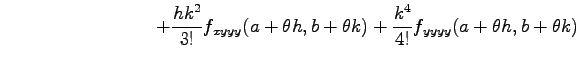 |
となる.
例 2.151 (テイラー展開)
関数
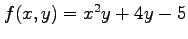 を点
を点 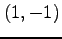 のまわりで
点
のまわりで
点 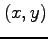 についてテイラー展開する.
まず,偏導関数は
についてテイラー展開する.
まず,偏導関数は
である.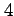 階以降の偏導関数はすべて 0 となる.
また,点
階以降の偏導関数はすべて 0 となる.
また,点 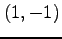 における偏微係数は
における偏微係数は
である.これを用いるとテイラー展開は
より,
となる. 多項式のテイラー展開は,多項式を単に変形した形となる.
である.
である.これを用いるとテイラー展開は
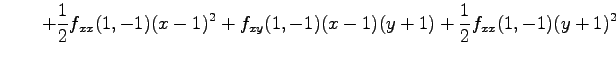 |
||
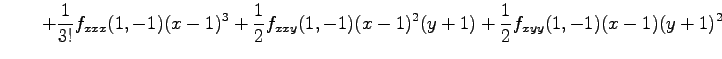 |
||
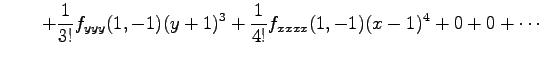 |
より,
となる. 多項式のテイラー展開は,多項式を単に変形した形となる.
例 2.152 (テイラー展開)
関数
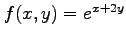 を点
を点 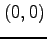 まわりで
点
まわりで
点 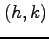 についてテイラー展開する.
まず,偏導関数は
についてテイラー展開する.
まず,偏導関数は
である.
となるから, 次項までのテイラー展開は
次項までのテイラー展開は
となる. 同様にして,
となるから, 次項までのテイラー展開は
次項までのテイラー展開は
となる.
である.
となるから,
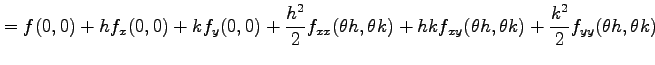 |
||
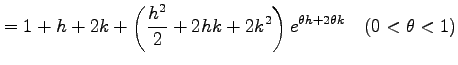 |
となる. 同様にして,
となるから,
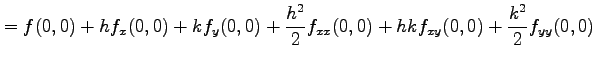 |
||
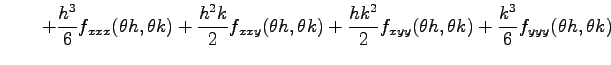 |
||
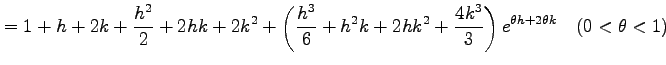 |
となる.
例 2.153 (テイラー展開)
関数
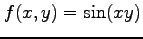 を点
を点
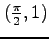 のまわりで
点
のまわりで
点 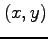 についてテイラー展開する.
まず,
についてテイラー展開する.
まず,
より,
となるので,テイラー展開は
である.展開を途中で打ち切ると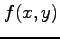 の
の 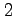 次の近似式
次の近似式 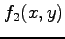 が
が
と得られる.
より,
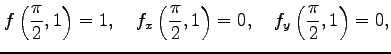 |
||
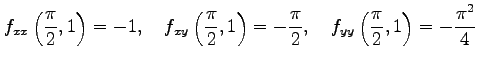 |
となるので,テイラー展開は
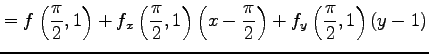 |
||
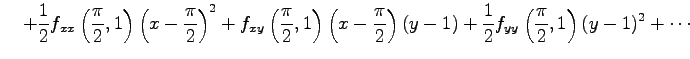 |
||
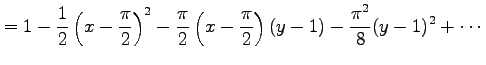 |
である.展開を途中で打ち切ると
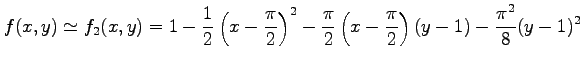 |
と得られる.
例 2.154 (テイラー展開)
関数
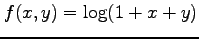 の
マクローリン展開を求める.
まず,
の
マクローリン展開を求める.
まず,
より,
となるので,マクローリン展開は
と得られる.
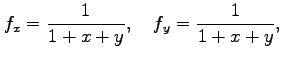 |
||
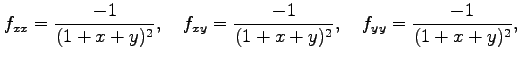 |
||
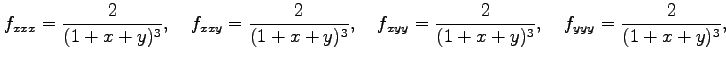 |
||
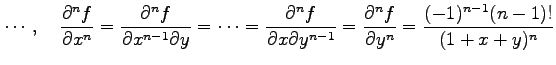 |
より,
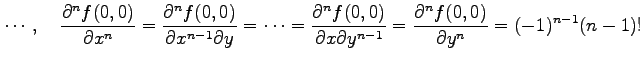 |
となるので,マクローリン展開は
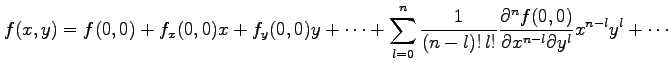 |
||
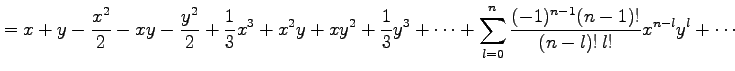 |
と得られる.
平成21年1月14日