4.18 正項級数に関する収束性の比較判定法
定理 4.63 (比較判定法)
二つの正項級数
を考える.
をみたすとき, 次の関係が成り立つ:
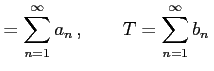 |
を考える.
数列 ![]() ,
, ![]() がある正の整数
がある正の整数 ![]() に対して
に対して
をみたすとき, 次の関係が成り立つ:
- (i)
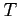 が収束するとき,
が収束するとき, も収束する.
も収束する.
- (ii)
 が発散するとき,
が発散するとき,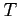 も発散する.
も発散する.
例 4.64 (比較判定法の具体例)
級数
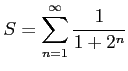 を考える.
数列
を考える.
数列
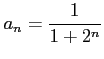 ,
,
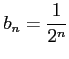 とする.
このとき
とする.
このとき
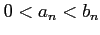 をみたす.
また,級数
をみたす.
また,級数
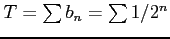 は収束する.
よって定理より級数
は収束する.
よって定理より級数
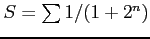 もまた収束する.
もまた収束する.
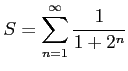 を考える.
数列
を考える.
数列
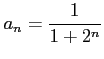 ,
,
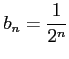 とする.
このとき
とする.
このとき
定理 4.65 (比較判定法)
二つの正項級数
を考える. 数列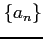 ,
, 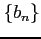 が
が
を満たし,かつ級数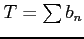 が収束するとき,
級数
が収束するとき,
級数
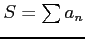 も収束する.
も収束する.
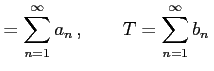 |
を考える. 数列
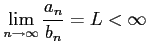 |
を満たし,かつ級数
例 4.66 (調和級数)
級数
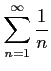 を
調和級数(harmonic series)という.
調和級数は発散する.
を
調和級数(harmonic series)という.
調和級数は発散する.
の各項を括り直して
とおき直す. ただし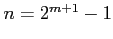 であり
であり
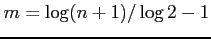 とおく.
ここで,数列
とおく.
ここで,数列
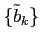 と
と
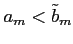 をみたす数列
をみたす数列 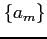 を
を
とおく. このとき,
が成り立つ.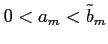 であり
であり
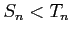 であるから,
比較判定法より
であるから,
比較判定法より
を得る.以上証明終り.
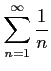 を
調和級数(harmonic series)という.
調和級数は発散する.
を
調和級数(harmonic series)という.
調和級数は発散する.
(証明)調和級数の部分和
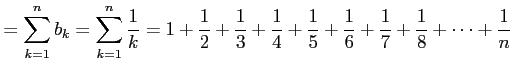 |
の各項を括り直して
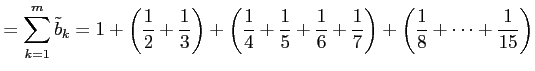 |
||
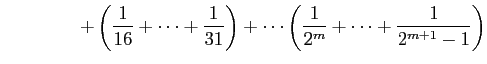 |
とおき直す. ただし
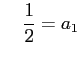 |
||||
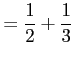 |
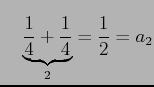 |
|||
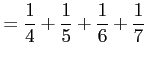 |
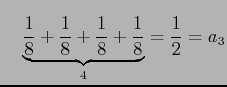 |
|||
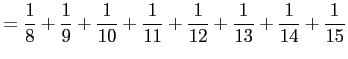 |
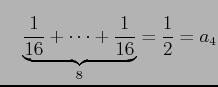 |
|||
 |
 |
|||
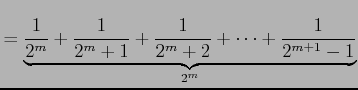 |
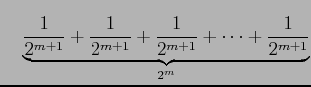 |
|||
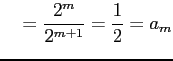 |
とおく. このとき,
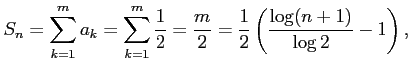 |
||
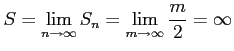 |
が成り立つ.
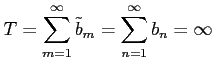 |
を得る.以上証明終り.
例 4.67 (収束判定の具体例)
級数
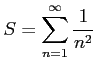 は
は
をみたす.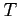 は収束するので,
は収束するので, も収束する.
も収束する.
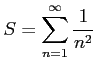 は
は
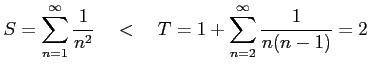 |
をみたす.
例 4.68 (収束判定の具体例)
級数
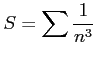 は
は
をみたす.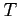 は収束するので
は収束するので  も収束する.
も収束する.
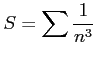 は
は
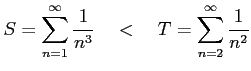 |
をみたす.
定理 4.69 (級数の収束)
 |
例 4.70 (比較判定法の具体例)
級数
は,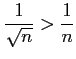 より,
より,
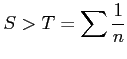 となる.
となる.
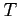 は発散するので
は発散するので  も発散する.
も発散する.
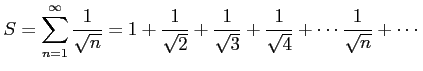 |
は,
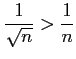 より,
より,
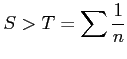 となる.
となる.
定理 4.71 (級数の収束)
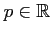 に対して
に対して
 |
例 4.72 (比較判定法)
級数
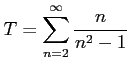 は
は
より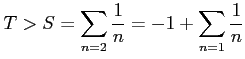 をみたす.
をみたす.
 は調和級数であり発散するので
は調和級数であり発散するので 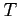 も発散する.
も発散する.
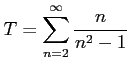 は
は
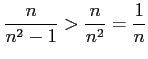 |
より
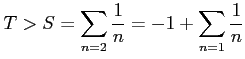 をみたす.
をみたす.
例 4.73 (比較判定法)
級数
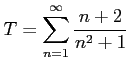 は
は
より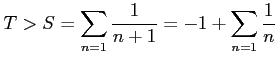 をみたす.
をみたす.
 は調和級数であり発散するので
は調和級数であり発散するので 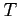 も発散する.
も発散する.
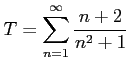 は
は
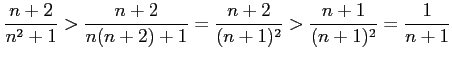 |
より
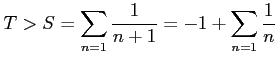 をみたす.
をみたす.
平成22年6月17日