4.24 演習 〜 級数,べき級数
問 4.105 (級数)
級数
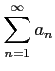 の定義を述べよ.
の定義を述べよ.
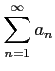 の定義を述べよ.
の定義を述べよ.
問 4.106 (級数)
次の級数について(i) 級数の第  部分和
部分和  を求めよ.
(ii) 数列
を求めよ.
(ii) 数列 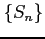 の概形を書け.
(iii) 級数の値を求めよ.
の概形を書け.
(iii) 級数の値を求めよ.
(1)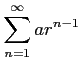 (2)
(2)
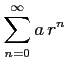 (3)
(3)
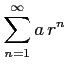 (4)
(4)
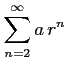 (5)
(5)
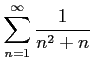 (6)
(6)
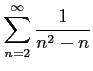
(7)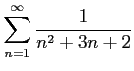 (8)
(8)
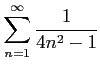 (9)
(9)
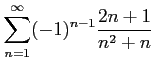
(1)
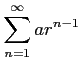 (2)
(2)
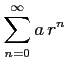 (3)
(3)
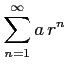 (4)
(4)
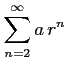 (5)
(5)
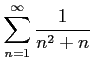 (6)
(6)
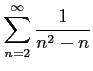
(7)
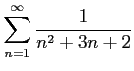 (8)
(8)
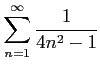 (9)
(9)
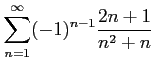
問 4.107 (級数)
次の級数の値を求めよ.
(1)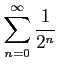 (2)
(2)
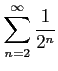 (3)
(3)
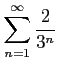 (4)
(4)
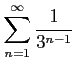 (5)
(5)
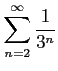 (6)
(6)
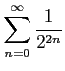 (7)
(7)
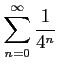
(8)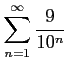 (9)
(9)
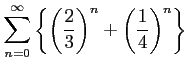 (10)
(10)
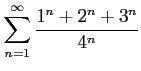 (11)
(11)
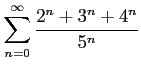
(12)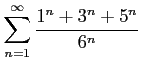 (13)
(13)
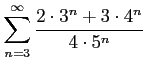 (14)
(14)
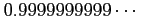
(1)
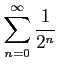 (2)
(2)
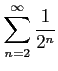 (3)
(3)
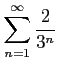 (4)
(4)
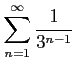 (5)
(5)
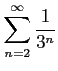 (6)
(6)
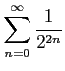 (7)
(7)
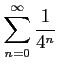
(8)
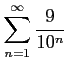 (9)
(9)
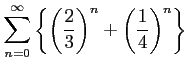 (10)
(10)
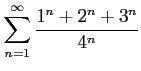 (11)
(11)
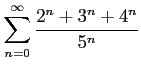
(12)
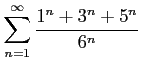 (13)
(13)
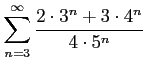 (14)
(14)
問 4.108 (比較判定)
次の級数は収束するか発散するか述べよ.
(1)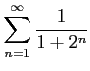 (2)
(2)
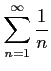 (3)
(3)
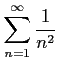 (4)
(4)
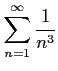 (5)
(5)
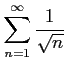 (6)
(6)
![$ \displaystyle{\sum_{n=1}^{\infty}\frac{1}{\sqrt[3]{n}}}$](img1978.png)
(7)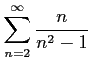 (8)
(8)
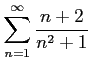
(1)
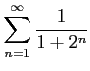 (2)
(2)
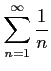 (3)
(3)
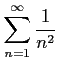 (4)
(4)
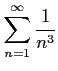 (5)
(5)
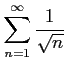 (6)
(6)
![$ \displaystyle{\sum_{n=1}^{\infty}\frac{1}{\sqrt[3]{n}}}$](img1978.png)
(7)
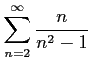 (8)
(8)
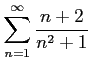
問 4.109 (ダランベールの収束判定)
次の級数は収束するか発散するか述べよ.
(1)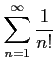 (2)
(2)
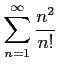 (3)
(3)
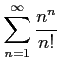 (4)
(4)
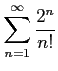 (5)
(5)
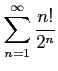 (6)
(6)
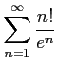 (7)
(7)
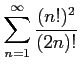
(8)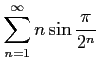 (9)
(9)
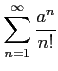 (
(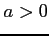 )
(10)
)
(10)
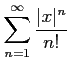 (
(
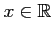 )
(11)
)
(11)
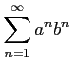 (
( )
)
(12)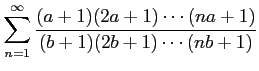 (
( )
)
(1)
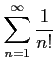 (2)
(2)
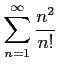 (3)
(3)
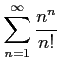 (4)
(4)
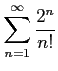 (5)
(5)
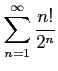 (6)
(6)
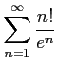 (7)
(7)
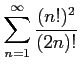
(8)
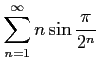 (9)
(9)
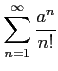 (
(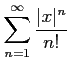 (
(
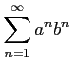 (
((12)
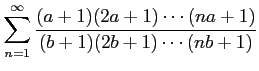 (
(
問 4.110 (コーシーの収束判定)
次の級数は収束するか発散するか述べよ.
(1)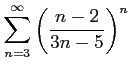 (2)
(2)
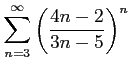 (3)
(3)
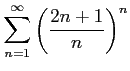 (4)
(4)
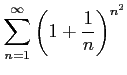
(5)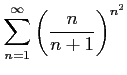 (6)
(6)
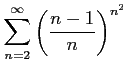 (7)
(7)
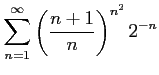 (8)
(8)
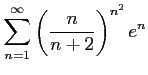
(9)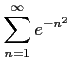 (10)
(10)
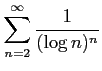
(1)
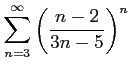 (2)
(2)
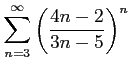 (3)
(3)
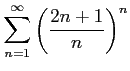 (4)
(4)
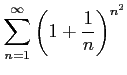
(5)
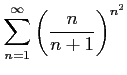 (6)
(6)
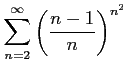 (7)
(7)
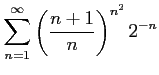 (8)
(8)
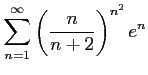
(9)
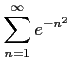 (10)
(10)
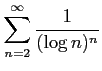
問 4.111 (交項級数)
次の級数は収束するか発散するか述べよ.
(1)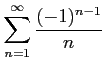 (2)
(2)
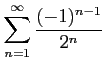
(1)
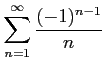 (2)
(2)
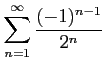
問 4.112 (級数の収束)
次の級数が絶対収束級数か条件収束級数か答えよ.
(1)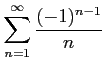 (2)
(2)
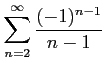 (3)
(3)
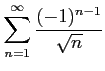 (4)
(4)
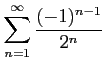 (5)
(5)
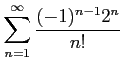
(6)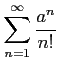 (
(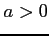 )
(7)
)
(7)
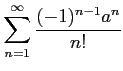 (
(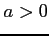 )
(8)
)
(8)
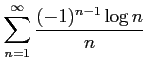 (9)
(9)
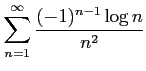
(10)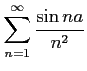
(1)
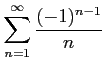 (2)
(2)
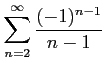 (3)
(3)
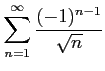 (4)
(4)
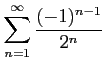 (5)
(5)
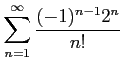
(6)
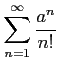 (
(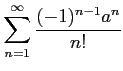 (
(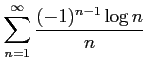 (9)
(9)
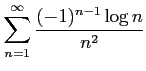
(10)
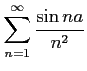
問 4.113 (べき級数)
べき級数
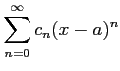 は
極限
は
極限
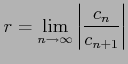 または
または
![$ \displaystyle{r= \lim_{n \to\infty}\frac{1}{\sqrt[n]{\vert c_n\vert}}}$](img2015.png) が存在するとき
が存在するとき
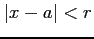 において絶対収束することを示せ.
において絶対収束することを示せ.
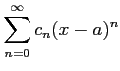 は
極限
は
極限
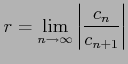 または
または
![$ \displaystyle{r= \lim_{n \to\infty}\frac{1}{\sqrt[n]{\vert c_n\vert}}}$](img2015.png) が存在するとき
が存在するとき
問 4.114 (べき級数)
次のべき級数の収束半径を求めよ.
(1)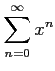 (2)
(2)
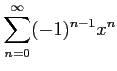
(3)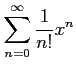 (4)
(4)
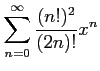 (5)
(5)
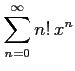 (6)
(6)
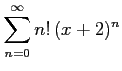 (7)
(7)
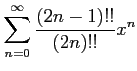
(8)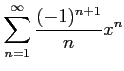 (9)
(9)
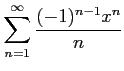 (10)
(10)
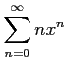 (11)
(11)
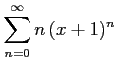 (12)
(12)
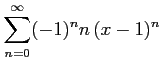
(13)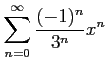 (14)
(14)
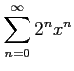 (15)
(15)
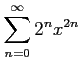 (16)
(16)
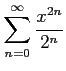 (17)
(17)
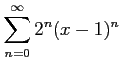
(18)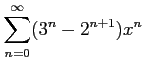 (19)
(19)
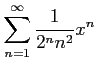 (20)
(20)
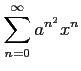 (
(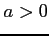 )
)
(21)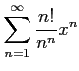 (22)
(22)
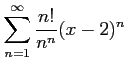 (23)
(23)
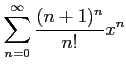 (24)
(24)
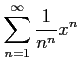 (25)
(25)
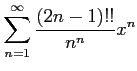
(26)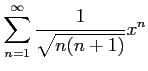 (27)
(27)
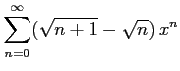
(1)
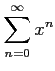 (2)
(2)
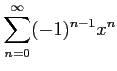
(3)
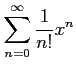 (4)
(4)
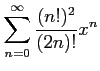 (5)
(5)
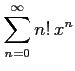 (6)
(6)
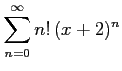 (7)
(7)
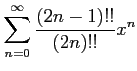
(8)
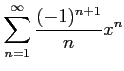 (9)
(9)
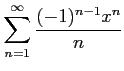 (10)
(10)
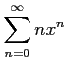 (11)
(11)
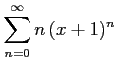 (12)
(12)
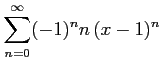
(13)
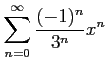 (14)
(14)
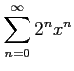 (15)
(15)
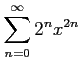 (16)
(16)
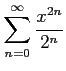 (17)
(17)
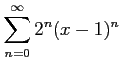
(18)
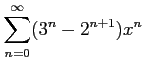 (19)
(19)
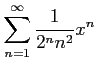 (20)
(20)
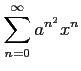 (
((21)
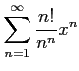 (22)
(22)
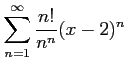 (23)
(23)
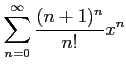 (24)
(24)
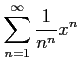 (25)
(25)
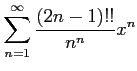
(26)
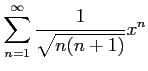 (27)
(27)
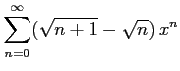
平成22年6月17日