2.2 極限
定義 2.8 (極限)
関数  において,
定義域内の点
において,
定義域内の点  を点
を点 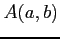 に近づけるとする.
ただし
に近づけるとする.
ただし
 とする.
このとき,
近づけ方に依らず
とする.
このとき,
近づけ方に依らず  が同じ 1 つの値
が同じ 1 つの値 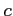 に近づくならば,
に近づくならば,
 は極限(limit)
は極限(limit) 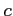 が存在する,
または,
が存在する,
または,
 は
は 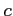 に収束する(convergent) といい,
に収束する(convergent) といい,
と表記する.
と表記する.
注意 2.9 (極限)
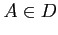 とは限らない.
とは限らない.
注意 2.10 (極限)
近づけ方によって, の値が異なるときは,極限が存在しない.
の値が異なるときは,極限が存在しない.
例 2.11 (極限)
関数
の原点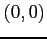 への極限を考える.
への極限を考える.
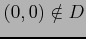 であることに注意する.
であることに注意する.
が成り立つ.
が成り立つ.
が成り立つ.
 |
の原点
(a) ![]() 軸(
軸(![]() の直線)に沿って近づける場合.
の直線)に沿って近づける場合.
![]() を代入した後に
を代入した後に ![]() の極限を考える.
このとき,
の極限を考える.
このとき,
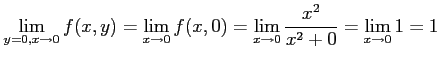 |
が成り立つ.
(b) ![]() 軸(
軸(![]() の直線)に沿って近づける場合.
の直線)に沿って近づける場合.
![]() を代入した後に
を代入した後に ![]() の極限を考える.
このとき,
の極限を考える.
このとき,
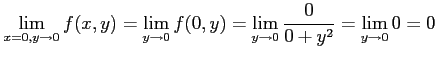 |
が成り立つ.
(c) 直線 ![]() に沿って近づける場合.
ただし,
に沿って近づける場合.
ただし,![]() は任意の実数とする.
は任意の実数とする.
![]() を代入した後に
を代入した後に ![]() の極限を考える.
このとき,
の極限を考える.
このとき,
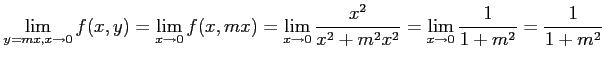 |
が成り立つ.
(a), (b), (c)より,
近づけ方が異なれば ![]() が近づく値も変わるので,
極限
が近づく値も変わるので,
極限
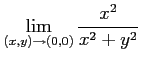 は存在しない.
は存在しない.
例 2.12 (極限)
関数
の原点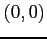 への極限を考える.
への極限を考える.
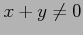 であることに注意する.
(a)
であることに注意する.
(a)  軸(
軸( の直線)に沿って近づける場合.
の直線)に沿って近づける場合.
 を代入した後に
を代入した後に 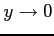 の極限を考える.
このとき,
の極限を考える.
このとき,
が成り立つ. (b) 直線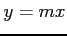 に沿って近づける場合.
ただし,
に沿って近づける場合.
ただし,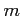 は
は 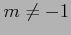 の任意の実数とする.
の任意の実数とする.
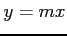 を代入した後に
を代入した後に 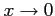 の極限を考える.
このとき,
の極限を考える.
このとき,
が成り立つ. ここで,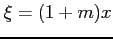 とおいた.
(a), (b), より,
全方向から近づけたとき同じ値
とおいた.
(a), (b), より,
全方向から近づけたとき同じ値  に収束するので,
極限
に収束するので,
極限
が存在する.
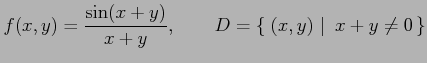 |
の原点
 |
が成り立つ. (b) 直線
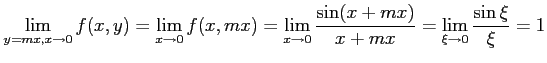 |
が成り立つ. ここで,
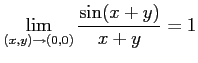 |
が存在する.
例 2.13 (極限)
関数
の原点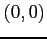 への極限を考える.
全方向から近づけるために,
への極限を考える.
全方向から近づけるために,
とおき, の極限を考える.
ただし,
の極限を考える.
ただし, は
は
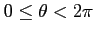 の
任意の実数とする.
このとき,
の
任意の実数とする.
このとき,
となり, 極限
が存在する.
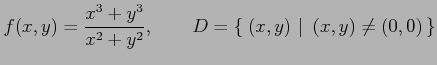 |
の原点
とおき,
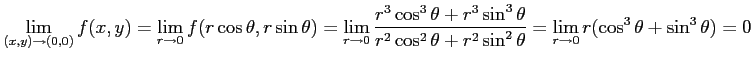 |
となり, 極限
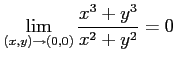 |
が存在する.
例 2.14 (極限)
関数
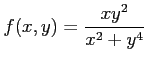 を考える.
この関数の定義域は一見すると
を考える.
この関数の定義域は一見すると
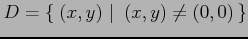 と見える.
しかし,
と見える.
しかし, のときを考えると,
のときを考えると,
となる.よって,この関数は正しくは,
となる.ただし,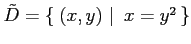 である.
定義域は
である.
定義域は 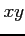 平面全体となる.
原点への極限は
平面全体となる.
原点への極限は  が領域
が領域 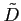 の中にないときは,
の中にないときは,
と極限が存在する. しかし, に対して常に
に対して常に
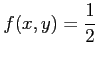 であり,
原点の近傍でもこれが成り立つ.
よって,原点への極限は存在しない.
であり,
原点の近傍でもこれが成り立つ.
よって,原点への極限は存在しない.
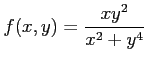 を考える.
この関数の定義域は一見すると
を考える.
この関数の定義域は一見すると
 |
となる.よって,この関数は正しくは,
![$\displaystyle f(x,y)= \begin{cases}\displaystyle{\frac{xy^2}{x^2+y^4}} & (x,y)\...
...in\tilde{D} \\ [1ex] \displaystyle{\frac{1}{2}} & (x,y)\in\tilde{D} \end{cases}$](img281.png) |
となる.ただし,
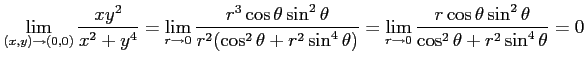 |
と極限が存在する. しかし,
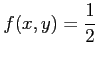 であり,
原点の近傍でもこれが成り立つ.
よって,原点への極限は存在しない.
であり,
原点の近傍でもこれが成り立つ.
よって,原点への極限は存在しない.
平成21年12月2日