三角関数

Next: 逆三角関数 Up: 変数と関数 Previous: 対数関数 Contents

三角関数

単位円（半径で中心が原点にある円）と原点を通る直線を用意する．円と直線の交点をとする．点より軸に下ろした垂線と軸との交点をとする．点をとし，を通り軸に平行な直線と直線との交点をとする．から点への円弧の（方向付き）長さをとする．このとき，点の座標を $(\cos x,\sin x)$ と定義し，点の座標を $(1,\tan x)$ と定義する．この定義により得られる関数を 三角関数（trigonometric function）と呼ぶ．読み方は $\sin x$ , $\cos x$ , $\tan x$ の順に sine, cosine, tangent である．
三角関数は

$\displaystyle \sin(x+2\pi)=\sin(x)\,,$ (150)

$\displaystyle \cos(x+2\pi)=\cos(x)\,,$ (151)

$\displaystyle \tan(x+\pi)=\tan(x)$ (152)

を満たすので $\sin x$ , $\cos x$ は周期 $2\pi$ の周期関数であり， $\tan x$ は周期 $\pi$ の周期関数である．また三角関数は

$\displaystyle \sin(-x)$ $\displaystyle =-\sin(x)\,,$ (153)

$\displaystyle \cos(-x)$ $\displaystyle =\cos(x)\,,$ (154)

$\displaystyle \tan(-x)$ $\displaystyle =-\tan(x)$ (155)

を満たすので， $\sin x$ , $\tan x$ は奇関数であり， $\cos x$ は偶関数である．さらに三角関数の性質を以下にいくつかあげる．まず $\overline{OP}^2=1$ より，

$\displaystyle \sin^2 x+\cos^2 x=1\,$ (156)

が成立する．三角関数はそれぞれ加法公式をもち，

$\displaystyle \sin(x\pm y)=\sin x \cos y \pm \cos x \sin y\,,$ (157)

$\displaystyle \cos(x\pm y)=\cos x \cos y \mp \sin x \sin y\,,$ (158)

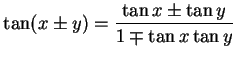$\displaystyle \tan(x\pm y)=\frac{\tan x\pm \tan y}{1\mp \tan x \tan y}\,$ (159)

となる．三角関数どうしの互いの関係は，

$\displaystyle \tan x=\frac{\sin x}{\cos x}\,,\quad \sin\left(\frac{\pi}{2}-x\ri... ...{2}-x\right)=\sin x\,,\quad \tan\left(\frac{\pi}{2}-x\right)=\frac{1}{\tan x}\,$ (160)

である．

問 2.17 教科書（p.26）問題 2-2 2.-3.

問 2.18 三角関数の概形を書け．

Next: 逆三角関数 Up: 変数と関数 Previous: 対数関数 Contents
Kondo Koichi
Created at 2002/09/12

	$\displaystyle \sin(x+2\pi)=\sin(x)\,,$	(150)
	$\displaystyle \cos(x+2\pi)=\cos(x)\,,$	(151)
	$\displaystyle \tan(x+\pi)=\tan(x)$	(152)

$\displaystyle \sin(-x)$	$\displaystyle =-\sin(x)\,,$	(153)
$\displaystyle \cos(-x)$	$\displaystyle =\cos(x)\,,$	(154)
$\displaystyle \tan(-x)$	$\displaystyle =-\tan(x)$	(155)

	$\displaystyle \sin(x\pm y)=\sin x \cos y \pm \cos x \sin y\,,$	(157)
	$\displaystyle \cos(x\pm y)=\cos x \cos y \mp \sin x \sin y\,,$	(158)
	$\displaystyle \tan(x\pm y)=\frac{\tan x\pm \tan y}{1\mp \tan x \tan y}\,$	(159)