Next: 逆双曲線関数 Up: 変数と関数 Previous: 逆三角関数 Contents
双曲線関数
双曲線関数(hyperbolic function)とは
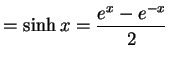 |
(167) | |
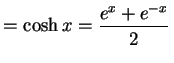 |
(168) | |
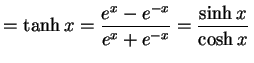 |
(169) |
により定義される関数である. 関数の読み方は上から hyperbolic sine, hyperbolic cosine, hyperbolic tangent である.
注意 2.20 (三角関数と双曲線関数)
三角関数は複素関数を用いて次のようにも定義される.
双曲線関数の定義との類似に注意せよ.
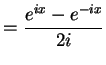 |
(170) | |
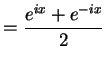 |
(171) | |
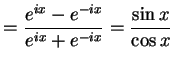 |
(172) |
双曲線関数の定義との類似に注意せよ.
問 2.21 (双曲線関数の概形)
双曲線関数の概形を書け.
定理 2.22 (双曲線関数の性質)
双曲線関数は次の性質をもつ.
| (173) | ||
| (174) | ||
| (175) | ||
| (176) | ||
| (177) | ||
| (178) | ||
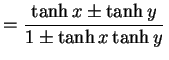 |
(179) |
問 2.23
この性質を証明せよ.
(証明)双曲線関数の定義をそのまま用いれば証明できる.
問 2.24 (双曲線関数の性質)
次の式を導け.
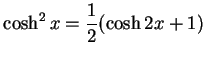 |
(180) | |
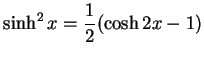 |
(181) | |
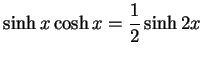 |
(182) | |
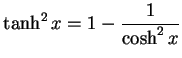 |
(183) |
問 2.25 (円と双曲線)
円 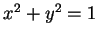 をパラメータ表示すると
をパラメータ表示すると
と表わせる. 双曲線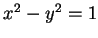 をパラメータ表示するには
をパラメータ表示するには
とおけばよい. これを示せ.
| (184) |
と表わせる. 双曲線
| (185) |
とおけばよい. これを示せ.
注意 2.26
双曲線関数に対して三角関数は円関数と呼ぶこともある.
Next: 逆双曲線関数 Up: 変数と関数 Previous: 逆三角関数 Contents
Kondo Koichi
Created at 2002/09/12