Next: 連続と不連続 Up: 変数と関数 Previous: 逆双曲線関数 Contents
関数の極限
定義 2.29 (右極限,左極限)
変数  を右から
を右から  に近づけたときの
に近づけたときの  の値を
の値を
と書き,右極限(right-hand limit)と呼ぶ. 同様に,変数 を左から
を左から  に近づけたときの値を
に近づけたときの値を
と書き,左極限(left-hand limit)と呼ぶ.
| (198) |
と書き,右極限(right-hand limit)と呼ぶ. 同様に,変数
| (199) |
と書き,左極限(left-hand limit)と呼ぶ.
定義 2.30 (関数の極限)
変数  を
を  に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
が成り立つとき, そのときに限り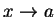 における関数
における関数  の極限が存在し,
の極限が存在し,
と書く. 極限が存在するとき以下のように表現する:
| (200) |
が成り立つとき, そのときに限り
と書く. 極限が存在するとき以下のように表現する:
| 関数 |
(202) | |
| (203) | ||
| (204) | ||
| (205) |
例 2.31 (関数の極限の具体例)
関数 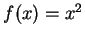 を考える.
このとき
を考える.
このとき
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
である.
| (206) |
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
| (207) |
である.
例 2.32 (関数の極限の具体例)
関数
を考える.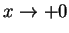 のとき
のとき
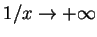 である.
である.
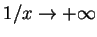 であるから
であるから  は
は 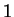 と
と 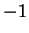 の間を振動する.
よって右極限
の間を振動する.
よって右極限
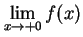 は存在しない.
は存在しない.
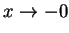 のとき
のとき
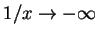 である.
以下同様で左極限
である.
以下同様で左極限
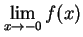 は存在しない.
右極限も左極限も存在しないので,
極限
は存在しない.
右極限も左極限も存在しないので,
極限
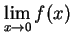 は存在しない.
は存在しない.
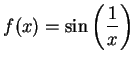 |
(208) |
を考える.
例 2.33 (関数の極限の具体例)
関数
を考える.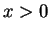 のとき
のとき
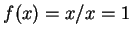 であるから
右極限は
であるから
右極限は
となる.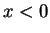 のとき
のとき
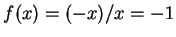 であるから
左極限は
であるから
左極限は
となる. 右極限と左極限が一致しないので, 極限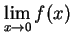 は存在しない.
は存在しない.
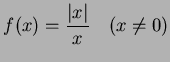 |
(209) |
を考える.
| (210) |
となる.
| (211) |
となる. 右極限と左極限が一致しないので, 極限
定理 2.34 (関数の極限に関する性質)
関数  ,
, 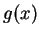 に関して極限
に関して極限
が存在するならば,
が成り立つ. ただし,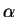 ,
,  は定数である.
は定数である.
| (212) |
が存在するならば,
| (213) | ||
| (214) | ||
| (215) | ||
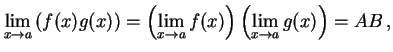 |
(216) | |
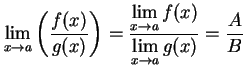 |
(217) |
が成り立つ. ただし,
例 2.35 (関数の極限の計算例)
| (218) | ||
| (219) | ||
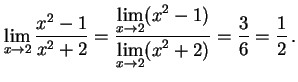 |
(220) |
変数 ![]() の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
![]() と書く.
変数
と書く.
変数 ![]() の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
![]() と書く.
また,
変数
と書く.
また,
変数 ![]() の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
![]() と書く.
変数
と書く.
変数 ![]() の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
![]() と書く.
と書く.
例 2.36 (関数の極限の計算例)
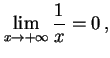 |
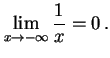 |
(221) | ||
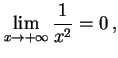 |
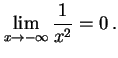 |
(222) | ||
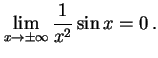 |
(223) | |||
| (224) | ||||
| (225) | ||||
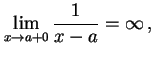 |
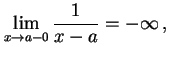 |
(226) | ||
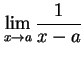 :存在ない :存在ない |
(227) | |||
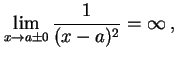 |
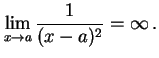 |
(228) | ||
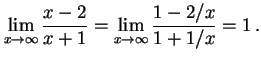 |
(229) | |||
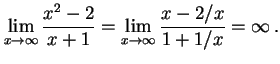 |
(230) |
公式 2.37 (ネピア数)
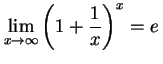 |
(231) |
公式 2.38
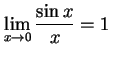 |
(232) |
問 2.39
教科書(p.31)問題 2-3.
Next: 連続と不連続 Up: 変数と関数 Previous: 逆双曲線関数 Contents
Kondo Koichi
Created at 2002/09/12