Next: コーシーの主値積分 Up: 積分法 Previous: 定積分の計算 Contents
広義積分
定義 5.14 (不連続点を含む区間での広義積分)
 で不連続
で不連続
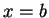 で不連続
で不連続
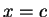
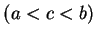 で不連続
で不連続
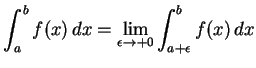 |
(720) |
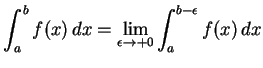 |
(721) |
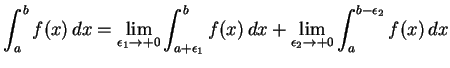 |
(722) |
定理 5.15
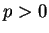
![$\displaystyle \int_{0}^{1}\frac{dx}{x^p}= \left\{\begin{array}{cc} \displaystyle{\frac{1}{1-p}} & (0<p<1) \\ [1em] +\infty & (p\geq1) \end{array}\right.$](img1426.png) |
(723) |
定義 5.16 (無限区間での広義積分)
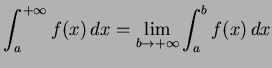 |
(724) | |
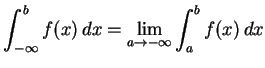 |
(725) | |
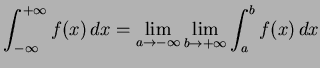 |
(726) |
定理 5.17
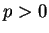
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^p}= \left\{\begin{array}{cc} +\infty & (0<p\leq1) \\ [1em] \displaystyle{\frac{1}{1-p}} & (p>1) \end{array}\right.$](img1430.png) |
(727) |
Kondo Koichi
Created at 2002/09/12