行列の簡約化

基本変形により連立一次方程式が

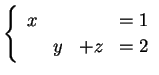$$\left\{\begin{array}{cccc} x & & & = 1 \\ & y & +z & = 2 \end{array}\right.$$ (149)

のように変形される場合は 掃き出し法では解が得られない． このような場合は 次の行列の簡約化により解を求める．

定義 2.5 (簡約な行列)   行列が

$$\left[\begin{array}{cccccccc} \!1\! & ** & \!0\! & ** & \!0\! & *... ... \\ \vdots& & & & & & &\vdots\\ 0 &\cdots& & & & &\cdots & 0 \end{array}\right]$$ (150)

という形をしているとき， この行列を簡約な行列と呼ぶ． 基本変形により行列を簡約な行列に変換することを簡約化と呼ぶ． また， 各行の一番左の 0 ではない成分を主成分と呼ぶ．

例 2.7 (簡約な行列の具体例)   次の行列は簡約な行列である：

$$\begin{bmatrix}0 & 1 & 3 & 0 & 2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & ... ...& 2 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\,,\quad$$ (151)

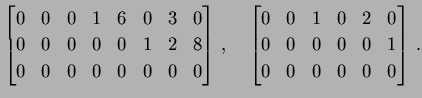$$\begin{bmatrix}0 & 0 & 0 & 1 & 6 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0... ... & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\,.$$ (152)

例 2.8   例題 2.2.1

定理 2.2 (簡約化の一意性)   任意の行列は基本変形により一意に簡約化できる．

例 2.9 (簡約化の計算例)  

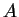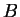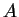定義 2.6 (行列の階数)   行列 $A$ を簡約化した行列を $B$ とする． このとき 行列 $A$ に対する行列の階数（rank）を

$$\mathrm{rank}\,(A) = B$$ (153)

と定義する．

例 2.10 (階数の具体例)  

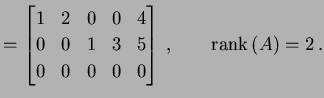$$A = \begin{bmatrix}1 & 2 & 0 & 0 & 4 \\ 0 & 0 & 1 & 3 & 5 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}\,,\qquad \mathrm{rank}\,(A)=2\,.$$ (154)

例 2.11 (階数の具体例)  

定理 2.3 (階数に関する定理)   行列 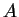$A$ が $m\times n$ 型のとき，

$$\mathrm{rank}\,(A)\le m\,, \qquad \mathrm{rank}\,(A)\le n\,$$ (155)

が成り立つ．

問 2.4   これを示せ．

問 2.5   教科書（p.27）問題2.2．

Kondo Koichi
Created at 2002/07/22