Next: 行列式 Up: 連立一次方程式 Previous: 行列の基本変形 Contents
逆行列
定義 2.9 (逆行列)
行列 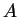 に対して
に対して
を満たす行列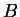 が存在するとき,
行列
が存在するとき,
行列 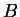 を行列
を行列 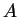 の逆行列(inverse matrix)と呼ぶ.
の逆行列(inverse matrix)と呼ぶ.
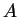 の逆行列は
の逆行列は 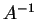 と表記する.
と表記する.
| (226) |
を満たす行列
問 2.8
逆行列をもつのは正方行列のみである.
これを示せ.
(証明)
![]() を満たす行列は可換な行列である.
可換な行列は正方行列のみである.
を満たす行列は可換な行列である.
可換な行列は正方行列のみである.
定理 2.10 (逆行列の一意性)
行列 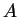 が逆行列をもつとき,逆行列は一意に定まる.
が逆行列をもつとき,逆行列は一意に定まる.
となる.よって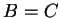 であり
であり 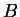 と
と 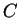 とは一致する.
とは一致する.
(証明)
![]() と
と ![]() が
が ![]() の逆行列であると仮定する.
このとき
の逆行列であると仮定する.
このとき ![]() ,
, ![]() が成り立つ.
これを用いて
が成り立つ.
これを用いて
| (227) |
となる.よって
定義 2.10 (行列の正則性)
正方行列 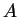 が逆行列をもつとき,
が逆行列をもつとき,
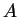 は正則(regular)であるという.
正則な行列を正則行列(regular matrix)と呼ぶ.
は正則(regular)であるという.
正則な行列を正則行列(regular matrix)と呼ぶ.
定理 2.11 (逆行列をもつ十分条件)
正方行列 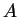 ,
, 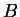 が
が 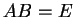 または
または 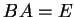 の
どちらか一方だけを満たすときでも
の
どちらか一方だけを満たすときでも
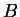 は
は 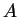 の逆行列となる.
の逆行列となる.
(証明)
証明はずっとあとに行なう.
定理 2.12 (逆行列の計算法)
行列 ![$ [A\vert E]$](img457.png) を簡約化して
を簡約化して ![$ [E\vert B]$](img458.png) の形に変形できたとする.
このとき
の形に変形できたとする.
このとき 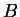 は
は 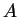 の逆行列
の逆行列 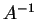 となる.
となる.
と書ける.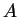 の左にかかっている行列をまとめて
の左にかかっている行列をまとめて 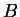 と書くと,
と書くと,
となる. この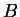 を用いれば
を用いれば 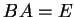 が成り立つ.
前述の定理より
が成り立つ.
前述の定理より 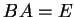 のとき
のとき 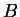 は
は 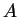 の逆行列
の逆行列 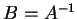 となる.
よって行列
となる.
よって行列 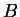 を求めればよい.
を求めればよい.
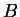 は
は
と書ける. これはすなわち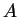 に行なった基本変形と同じ操作を
に行なった基本変形と同じ操作を 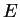 に
対して行なうことを意味する.
これらの操作を同時に行なうには,
行列
に
対して行なうことを意味する.
これらの操作を同時に行なうには,
行列 ![$ [A\vert E]$](img457.png) を考えて
を考えて ![$ [E\vert B]$](img458.png) の形に簡約化すればよい.
この一連の操作により
の形に簡約化すればよい.
この一連の操作により 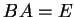 を得る.
を得る.
(証明)
行列 ![]() に基本変形を繰り返し行ない単位行列
に基本変形を繰り返し行ない単位行列 ![]() に変換されたとする.
このとき
に変換されたとする.
このとき
| (228) |
と書ける.
| (229) |
となる. この
| (230) |
と書ける. これはすなわち
例 2.17 (逆行列の計算例)
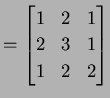 |
(231) |
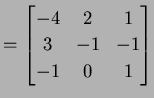 |
(232) |
定理 2.13 (行列の正則性と緒性質)
正方行列 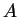 に対して次の(1)-(5) は同値である:
に対して次の(1)-(5) は同値である:
- (1)
-
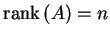 .
.
- (2)
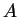 の簡約化は
の簡約化は 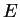 である.
である.
- (3)
-
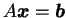 は任意の
は任意の 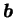 に対して唯一つの解をもつ.
に対して唯一つの解をもつ.
- (4)
-
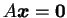 は自明な解
は自明な解
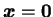 のみをもつ.
のみをもつ.
- (5)
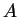 は正則である.
は正則である.
定理 2.14
正方行列 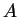 が正則なとき方程式
が正則なとき方程式
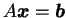 は
解
は
解
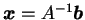 をもつ.
をもつ.
例 2.18 (逆行列をもたない具体例)
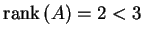 となるので
となるので  は正則ではない.
よって
は正則ではない.
よって  は逆行列をもたない.
は逆行列をもたない.
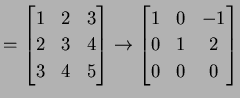 |
(233) |
例 2.19 (逆行列を用いた解法の具体例)
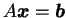 とすると
とすると
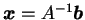 より
解が求まる.
より
解が求まる.
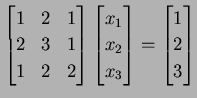 |
(234) |
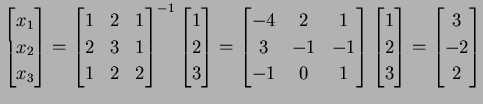 |
(235) |
定理 2.15 (逆行列の性質)
正方行列 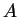 ,
, 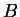 が正則のとき次の関係式が成り立つ.
が正則のとき次の関係式が成り立つ.
- (1)
-
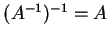 .
.
- (2)
-
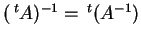 .
.
- (3)
-
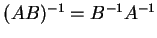 .
.
問 2.9
これを示せ.
(証明)
(3) を示す.
Next: 行列式 Up: 連立一次方程式 Previous: 行列の基本変形 Contents
Kondo Koichi
Created at 2002/07/22