Next: 逆行列 Up: 連立一次方程式 Previous: ちょっとまとめ Contents
行列の基本変形
定理 2.9 (行列の積による行列の行の基本変形)
行列
![$ A=[a_{ij}]_{m\times n}$](img134.png) が与えられたとき,
次に定義される行列
が与えられたとき,
次に定義される行列
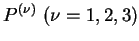 を左から掛けて,
積
を左から掛けて,
積
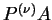 を考える.
このとき
を考える.
このとき
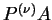 は行列の行の第
は行列の行の第 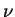 基本変形を
基本変形を
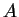 にほどこした行列と等しい.
にほどこした行列と等しい.
- (1)
- 第
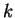 行を
行を 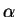 倍する.
倍する.
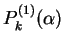
![$\displaystyle = \underset{k}{ \left[\begin{array}{ccc\vert c\vert ccc} \!1\! & ...
...[-.5ex] & & & & & \!\ddots\! & \\ [-.5ex] & & & & & & \!1\! \end{array}\right]}$](img408.png)
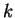
(202)
- (2)
- 第
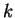 行と第
行と第 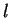 行を入れ替える.
行を入れ替える.
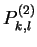
![$\displaystyle = \underset{k\qquad\qquad\,\,\,l}{ \left[\begin{array}{ccc\vert c...
...& & & & & & & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}$](img411.png)
(203)
- (3)
- 第
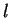 行を
行を 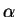 倍して第
倍して第 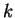 行に加える.
行に加える.
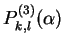
![$\displaystyle = \underset{k\qquad\qquad\,\,\,l}{ \left[\begin{array}{ccc\vert c...
...& & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}\quad(k<l)$](img413.png)
(204)
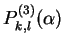
![$\displaystyle = \underset{l\qquad\qquad\,\,\,k}{ \left[\begin{array}{ccc\vert c...
...& & \!\ddots\! & \\ [-.5ex] & & & & & & & & & & 1 \end{array}\right]}\quad(l<k)$](img414.png)
(205)
問 2.6
これを示せ.
例 2.15 (行列の行の基本変形の具体例)
行列
を考える. このとき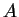 にいろいろな基本変形を行なうと次のようになる.
にいろいろな基本変形を行なうと次のようになる.
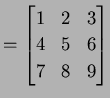 |
(206) |
を考える. このとき
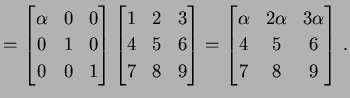 ← 第 ← 第 |
(207) | |
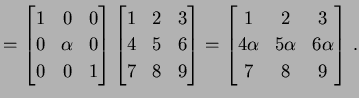 ← 第 ← 第 |
(208) | |
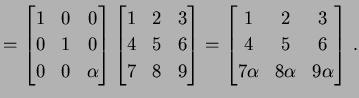 ← 第 ← 第 |
(209) | |
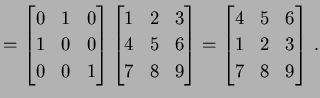 ← 第 ← 第 |
(210) | |
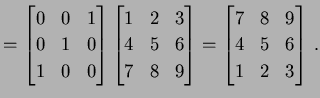 ← 第 ← 第 |
(211) | |
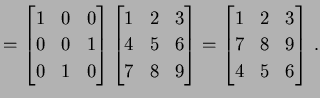 ← 第 ← 第 |
(212) | |
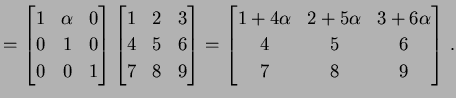 |
(213) | |
| ← 第 |
(214) | |
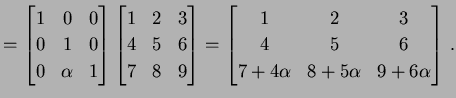 |
(215) | |
| ← 第 |
(216) | |
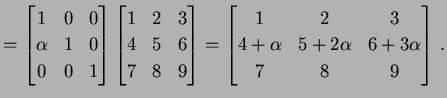 |
(217) | |
| ← 第 |
(218) |
例 2.16 (上三角化,対角化)
行列
に左から行列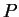 をかけて上三角行列
をかけて上三角行列
に変換する. すなわち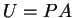 をみたす行列
をみたす行列 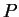 を求める.
次に
を求める.
次に 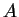 に左から行列
に左から行列 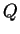 をかけて
単位行列
をかけて
単位行列
に変換する. すなわち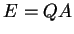 をみたす行列
をみたす行列 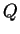 を求める.
を求める.
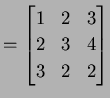 |
(219) |
に左から行列
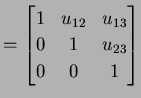 |
(220) |
に変換する. すなわち
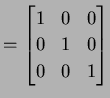 |
(221) |
に変換する. すなわち
まず ![]() を求める.
を求める.
![]() に左から行列
に左から行列 ![]() (
(![]() ) をかけて
基本変形を行なう.
) をかけて
基本変形を行なう.
| (222) |
| (223) |
問 2.7 (下三角化)
行列
に左から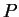 をかけて
下三角行列
をかけて
下三角行列
に変換せよ. すなわち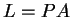 を満たす行列
を満たす行列 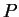 を求めよ.
を求めよ.
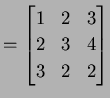 |
(224) |
に左から
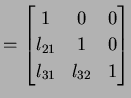 |
(225) |
に変換せよ. すなわち
Next: 逆行列 Up: 連立一次方程式 Previous: ちょっとまとめ Contents
Kondo Koichi
Created at 2002/07/22