Next: 多項式の文字の置換 Up: 行列式 Previous: 行列式 Contents
置換
定義 3.1 (文字の置換)
 個の文字
個の文字
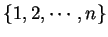 から
自分自身
から
自分自身
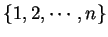 への
への
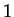 対
対 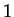 の写像を
の写像を
 文字の置換(permutation)という.
文字の置換(permutation)という.
 文字の置換
文字の置換 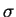 が写像
が写像
のとき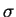 を
を
と表わす. 写像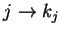 を
を
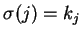 と表わす.
と表わす.
| (236) |
のとき
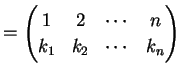 |
(237) |
と表わす. 写像
例 3.1 (置換の具体例)
例 3.2 (置換の表記)
定義 3.2 (置換の積)
置換 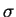 ,
, 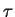 の積
の積
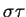 を
を
または
と定義する.
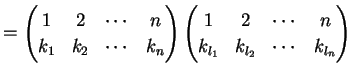 |
(238) |
または
| (239) |
と定義する.
例 3.3 (置換の積の具体例)
注意 3.1 (置換の積は非可換)
一般的に
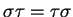 は成立しない.
は成立しない.
定義 3.3 (単位置換)
全ての文字を動かさない置換
を単位置換と呼ぶ.
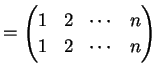 |
(240) |
を単位置換と呼ぶ.
定義 3.4 (逆置換)
置換 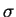 に対して
に対して
を満たす置換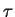 を
を 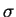 の逆置換と呼び,
の逆置換と呼び,
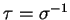 と表わす.
と表わす.
| (241) |
を満たす置換
定理 3.1 (逆置換)
置換
の逆置換は
で与えられる.
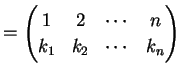 |
(242) |
の逆置換は
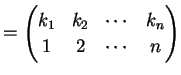 |
(243) |
で与えられる.
例 3.4 (逆置換の具体例)
定義 3.5 (巡回置換)
 個の文字
個の文字
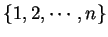 のうち
のうち
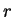 個の文字
個の文字
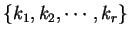 のみを
のみを
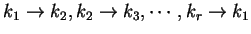 と順にずらし,
残りの文字
と順にずらし,
残りの文字
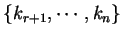 を
を
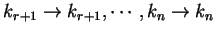 と動かさない
写像の置換を巡回置換という.
巡回置換は
と動かさない
写像の置換を巡回置換という.
巡回置換は
と表わされ,省略するときは
と書く.
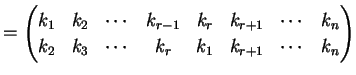 |
(244) | |
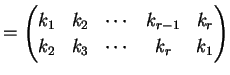 |
(245) |
と表わされ,省略するときは
| (246) |
と書く.
例 3.5 (巡回置換の具体例)
定理 3.2 (置換を巡回置換の積で表わす)
任意の置換 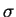 は巡回置換
は巡回置換
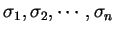 の積
の積
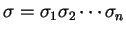 で表わされる.
で表わされる.
例 3.6 (置換を巡回置換の積で表わす計算例)
定義 3.6 (互換)
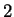 文字の巡回置換
文字の巡回置換 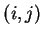 を互換という.
を互換という.
定理 3.3 (巡回置換を互換の積で表わす)
任意の巡回置換は互換の積で表わされる.
たとえば,その一つとして
と表わされる.
| (247) |
と表わされる.
例 3.7 (置換を互換の積で表わす)
注意 3.2
互換の積で表わす方法は幾通りもある.
定義 3.7 (置換の符号)
置換 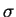 が
が 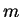 個の互換の積で表わされるとき
個の互換の積で表わされるとき
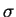 の符号(sign)を
の符号(sign)を
と定義する.
| (248) |
と定義する.
例 3.8 (置換の符号の具体例)
定理 3.4 (置換の符号の一意性)
置換 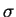 の符号
の符号
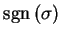 は
互換の積の表わし方によらず一意に定まる.
は
互換の積の表わし方によらず一意に定まる.
定理 3.5 (置換の符号の性質)
| (249) | ||
| (250) | ||
| (251) |
定義 3.8 (偶置換,奇置換)
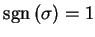 となる置換を
偶置換と呼び,
となる置換を
偶置換と呼び,
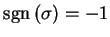 となる置換を
奇置換と呼ぶ.
となる置換を
奇置換と呼ぶ.
例 3.9 (偶置換,奇置換の具体例)
定義 3.9 (置換全体の集合)
 文字の置換
文字の置換 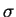 の全体の集合を
の全体の集合を 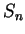 と書く.
と書く.
注意 3.3 (置換全体の集合の要素の個数)
 文字の置換は写像
文字の置換は写像
であるから, その個数は 個の文字の順列組合わせに等しい.
よって集合
個の文字の順列組合わせに等しい.
よって集合 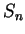 の個数は
の個数は 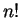 である.
である.
| (252) |
であるから, その個数は
例 3.10 (置換全体の集合の具体例)
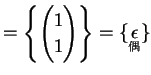 |
(253) | |
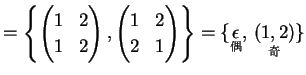 |
(254) | |
| (255) |
問 3.1
 次の置換全体の集合
次の置換全体の集合 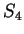 の要素全てを書き出せ.
またその偶奇も述べよ.
の要素全てを書き出せ.
またその偶奇も述べよ.
問 3.2
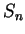
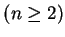 に含まれる偶置換と奇置換の個数は等しい.
これを示せ.
に含まれる偶置換と奇置換の個数は等しい.
これを示せ.
Next: 多項式の文字の置換 Up: 行列式 Previous: 行列式 Contents
Kondo Koichi
Created at 2002/07/22