Next: 行列式の定義 Up: 行列式 Previous: 置換 Contents
多項式の文字の置換
定義 3.10 (多項式の変数の置換)
o 変数
変数 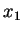 ,
, 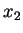 ,
, 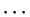 ,
, 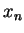 の
多項式
の
多項式
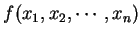 と
置換
と
置換
 に対して
に対して
と定義する.
| (256) |
と定義する.
例 3.11 (多項式の変数の置換の具体例)
定理 3.6 (置換の積)
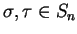 に対して
に対して
が成立する.
| (257) |
が成立する.
(証明)
定義 3.11 (差積)
 変数
変数
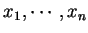 の多項式
の多項式
を差積と呼ぶ.
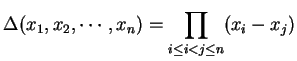 |
(258) |
を差積と呼ぶ.
例 3.12 (差積の具体例)
定理 3.7 (互換による差積の置換)
互換
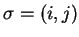 に対して
に対して
が成立する.
| (259) |
が成立する.
(証明)
定理 3.8 (差積の変数の置換)
置換
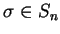 に対して
に対して
が成立する.
| (260) |
が成立する.
(証明)
定理 3.9 (置換の符号の一意性)
置換の符号は互換の積の表わし方によらず一意に定まる.
(証明)
Kondo Koichi
Created at 2002/07/22