Next: 行ベクトル,列ベクトル Up: 行列とベクトル Previous: 行列 Contents
行列のいろいろ
定義 1.2 (零行列)
成分が全て零の行列
を零行列(zero matrix)と呼ぶ.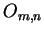 は
は  型の零行列を意味する.
型の零行列を意味する.
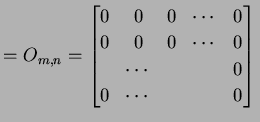 |
(5) |
を零行列(zero matrix)と呼ぶ.
定義 1.3 (正方行列)
行と列の数が等しい行列
を正方行列(square matrix)と呼ぶ. 行列の成分のうち左上から右下へ並んでいる成分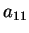 ,
,
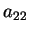 ,
, 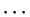 ,
, 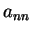 を
対角成分(diagonal components)と呼ぶ.
を
対角成分(diagonal components)と呼ぶ.
 |
(6) |
を正方行列(square matrix)と呼ぶ. 行列の成分のうち左上から右下へ並んでいる成分
定義 1.4 (対角行列)
対角成分以外の成分が全て零の正方行列
を対角行列(diagonal matrix)と呼ぶ.
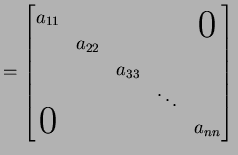 |
(7) |
を対角行列(diagonal matrix)と呼ぶ.
定義 1.5 (単位行列)
対角成分がすべて 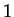 の対角行列
の対角行列
を単位行列(unit matrix)と呼ぶ.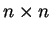 の単位行列を
の単位行列を 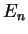 と書き
と書き  次の単位行列と呼ぶ.
単位行列は後述するように行列の積において ``
次の単位行列と呼ぶ.
単位行列は後述するように行列の積において `` '' の役割をはたす.
'' の役割をはたす.
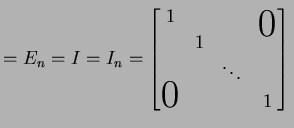 |
(8) |
を単位行列(unit matrix)と呼ぶ.
定義 1.6 (スカラー行列)
対角成分の値がすべて等しい対角行列を
スカラー行列(scalar matrix)と呼ぶ.
例 1.1 (スカラー行列の具体例)
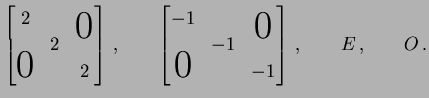 |
(9) |
定義 1.7 (上三角行列)
対角成分を除く左下半分がすべて 0 の正方行列
を上三角行列(upper triangular matrix)と呼ぶ.
 |
(10) |
を上三角行列(upper triangular matrix)と呼ぶ.
定義 1.8 (下三角行列)
対角成分を除く右上半分がすべて 0 の正方行列
を下三角行列(lower triangular matrix)と呼ぶ.
 |
(11) |
を下三角行列(lower triangular matrix)と呼ぶ.
定義 1.9 (転置行列)
行と列の成分を入れ換えた行列
を転置行列(transposed matrix)と呼ぶ. 行と列を入れ換える演算を転置(transpose)をとるという. 転置された行列を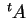 と書く.また
と書く.また 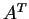 と書くこともある.
と書くこともある.
 |
(12) |
を転置行列(transposed matrix)と呼ぶ. 行と列を入れ換える演算を転置(transpose)をとるという. 転置された行列を
例 1.2 (転置の具体例)
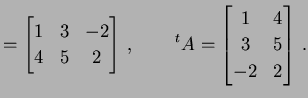 |
(13) |
問 1.1
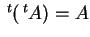 を示せ.
を示せ.
となる.証明終了.
(証明)
![]() ,
,
![]() とおく.
行と列を入れ換えるので
とおく.
行と列を入れ換えるので ![]() は
は
![]() とも書ける.
つまり
とも書ける.
つまり
![]() となる.
転置をとる操作を成分でみると,
行と列の添字を入れ換える操作に対応する.
よって
となる.
転置をとる操作を成分でみると,
行と列の添字を入れ換える操作に対応する.
よって
| (14) |
となる.証明終了.
定義 1.10 (対称行列)
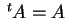 を満たす行列を
対称行列(symmetric matrix)と呼ぶ.
を満たす行列を
対称行列(symmetric matrix)と呼ぶ.
例 1.3 (対称行列の具体例)
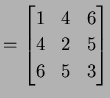 |
(15) |
問 1.2 (対称行列の一般的な表現)
対称行列は正方行列で一般に
と表わされる. これを示せ.
 |
(16) |
と表わされる. これを示せ.
定義 1.11 (歪対称行列)
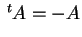 を満たす行列を
歪対称行列(skew symmetric matrix)
または,
交代行列(alternative matrix)
と呼ぶ.
を満たす行列を
歪対称行列(skew symmetric matrix)
または,
交代行列(alternative matrix)
と呼ぶ.
例 1.4 (歪対称行列の具体例)
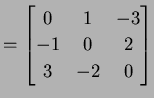 |
(17) |
問 1.3 (対称行列の一般的な表現)
歪対称行列は正方行列で一般に
と表わされる. これを示せ.
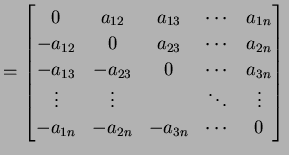 |
(18) |
と表わされる. これを示せ.
問 1.4
教科書(p.5)問題 1.1.
Next: 行ベクトル,列ベクトル Up: 行列とベクトル Previous: 行列 Contents
Kondo Koichi
Created at 2002/07/22