Next: 13 正項級数 Up: 1 数列と極限 Previous: 11 数列の有界性と単調性 Contents
12 級数
級数(series)とは数列 ![]() の和である.
式では
の和である.
式では
| (74) | ||
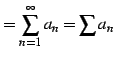 |
(75) |
と書き表す. 加法(足し算)は有限回の演算においてのみ定義されているので, 式(
| (76) |
を考える. これを第
| (77) |
を考える. 数列
| (78) |
が存在したとする. このとき級数
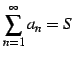 |
(79) |
で与えられると定義する. 極限
定義 1.41 (級数)
数列 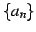 の和
の和
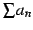 を級数(series)と呼び,
その値は
を級数(series)と呼び,
その値は
で定義する. この極限が存在するとき 級数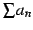 は収束する(convergent)といい,
収束しない場合を
級数
は収束する(convergent)といい,
収束しない場合を
級数
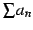 は発散する(divergent)という.
は発散する(divergent)という.
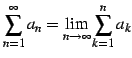 |
(80) |
で定義する. この極限が存在するとき 級数
例 1.44 (無限級数の結合則)
数列
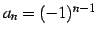 の
級数
の
級数
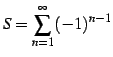 を考える.
すなわち
を考える.
すなわち
である. 足し算の順を入れ替えると
となる.また別の順で足し合わせると
となる. これらは矛盾する. どこが誤りであろうか? 有限の項の和の常識は無限の項の和には通用しない. この場合の間違いは足し算の順を変えたことである. この例では結合則が成り立たない. 定義![[*]](./icons/crossref.png) に従えば級数
に従えば級数 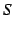 は発散である.
は発散である.
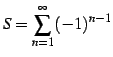 を考える.
すなわち
を考える.
すなわち
| (82) |
である. 足し算の順を入れ替えると
| (83) | ||
| (84) |
となる.また別の順で足し合わせると
| (85) | ||
| (86) |
となる. これらは矛盾する. どこが誤りであろうか? 有限の項の和の常識は無限の項の和には通用しない. この場合の間違いは足し算の順を変えたことである. この例では結合則が成り立たない. 定義
例 1.45 (等比級数)
等比数列
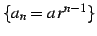 の無限和を
等比級数(geometrical progression series)と呼び,
の無限和を
等比級数(geometrical progression series)と呼び,
と書き表す. 等比級数は
となる.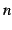 部分和
部分和
を考える.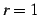 のとき,
のとき,
となる. つぎに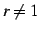 のとき,等式
のとき,等式
を用いると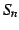 は
は
と書ける. 以上より
となる. ただし無限大の符号は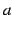 の符号
の符号
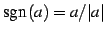 で決まる.
証明終り.
で決まる.
証明終り.
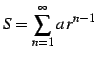 |
(87) |
と書き表す. 等比級数は
![$\displaystyle S=\left\{ \begin{array}{ll} \displaystyle{\frac{a}{1-r}} & (\vert r\vert< 1) \\ [1em] \text{発散} & (\vert r\vert\ge 1) \end{array} \right.$](img298.png) |
(88) |
となる.
(証明) 第
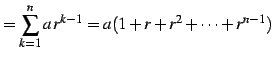 |
(89) |
を考える.
| (90) |
となる. つぎに
| (91) |
を用いると
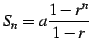 |
(92) |
と書ける. 以上より
![$\displaystyle S=\lim_{n\to\infty}S_{n}= \left\{ \begin{array}{lc} \displaystyle...
...& (-1<r<1)\\ [2ex] \displaystyle{\text{不確定}} & (r\leq-1) \end{array} \right.$](img308.png) |
(93) |
となる. ただし無限大の符号は
問 1.46 (1を根にもつ多項式の因数分解)
次の等式を示せ.
| (94) |
注意 1.47 (初項が異なる級数)
級数が
と定義されるときの値を考える. 部分和は
となるから, 結局級数は
と得られる.
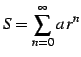 |
(95) |
と定義されるときの値を考える. 部分和は
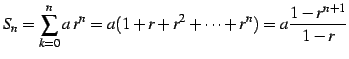 |
(96) |
となるから, 結局級数は
![$\displaystyle S= \lim_{n\to\infty}S_{n}= \lim_{n\to\infty}a\frac{1-r^{n+1}}{1-r...
...(\vert r\vert<1) \\ [1ex] \text{発散} & (\vert r\vert\geq1) \end{array} \right.$](img314.png) |
(97) |
と得られる.
注意 1.48 (等比級数の有理式表現)
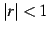 のとき
のとき
とな. この式は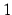 を
を 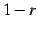 で割ることでも導出される.
すなわち,
で割ることでも導出される.
すなわち,
のように低次項を主項として割り算を無限回続ける.
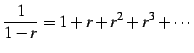 |
(98) |
とな. この式は
| (99) | ||
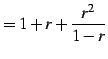 |
(100) | |
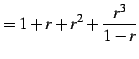 |
(101) | |
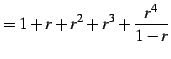 |
(102) | |
| (103) |
のように低次項を主項として割り算を無限回続ける.
例 1.49 (等比級数の具体例)
または
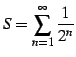 |
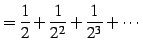 |
(104) |
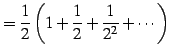 |
(105) | |
| (106) | ||
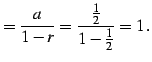 |
(107) |
または
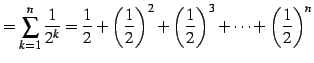 |
(108) | |
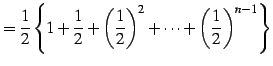 |
(109) | |
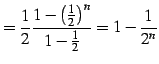 |
(110) |
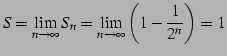 |
(111) |
例 1.50 (等比級数の具体例)
または
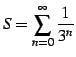 |
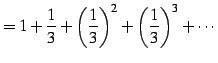 |
(112) |
| (113) | ||
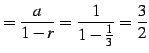 |
(114) |
または
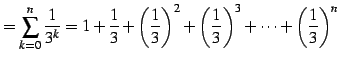 |
(115) | |
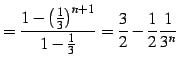 |
(116) |
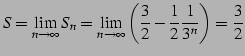 |
(117) |
例 1.51 (等比級数の具体例)
| (118) |
(証明)
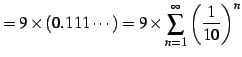 |
(119) | |
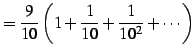 |
(120) | |
| (121) | ||
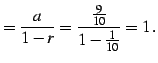 |
(122) |
問 1.52
参考書(p.172)問題7-1.
問 1.53 (級数の計算)
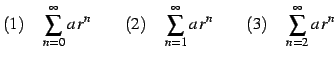 |
(123) | |
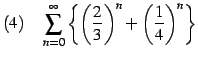 |
(124) | |
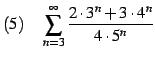 |
(125) | |
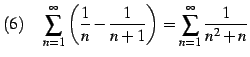 |
(126) |
Next: 13 正項級数 Up: 1 数列と極限 Previous: 11 数列の有界性と単調性 Contents
Kondo Koichi
Created at 2003/08/29