4 直線の方程式

一般に $\vec{x}\in\mathbb{R}^n$ のとき 直線の方程式は

$$\vec{x} =\vec{q}+t\,\vec{p}\,,\quad \forall t \in\mathbb{R}$$ (485)

と表される． $\vec{p}$ を方向ベクトル（tangent vector）という．

$\vec{x}\in\mathbb{R}^2$ のとき

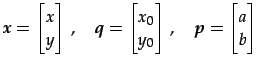$$\vec{x}= \begin{bmatrix}x \\ y \end{bmatrix}\,,\quad \vec{q}= \be... ...{0} \\ y_{0} \end{bmatrix}\,,\quad \vec{p}= \begin{bmatrix}a \\ b \end{bmatrix}$$ (486)

とすると 直線の方程式は

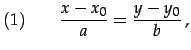$$(1)\qquad \frac{x-x_{0}}{a}=\frac{y-y_0}{b}\,,$$ (487)

$$(2)\qquad a'(x-x_{0})+b'(y-y_0)=0\,, (a'=b\,,b'=-a)$$ (488)

$$(3)\qquad y=y_{0}+a''(x-x_{0})\,, (a''=-a'/b'=b/a)$$ (489)

と表される． 式(2)は

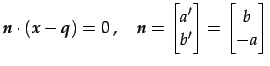$$\vec{n}\cdot(\vec{x}-\vec{q})=0\,,\quad \vec{n}= \begin{bmatrix}a' \\ b' \end{bmatrix}= \begin{bmatrix}b \\ -a \end{bmatrix}$$ (490)

とも表される． $\vec{n}$ を法線ベクトル（normal vector）という． $\vec{p}\cdot\vec{n}=0$ となることに注意する．

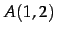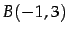問 4.43   点 $A(1,2)$, $B(-1,3)$ を通る直線の方程式を求めよ．

（答え）

$\vec{x}\in\mathbb{R}^3$ のとき

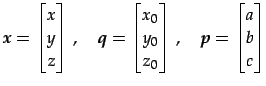$$\vec{x}= \begin{bmatrix}x \\ y \\ z \end{bmatrix}\,,\quad \vec{q}... ...\ z_{0} \end{bmatrix}\,,\quad \vec{p}= \begin{bmatrix}a \\ b \\ c \end{bmatrix}$$ (491)

とすると 直線の方程式は

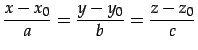$$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$$ (492)

と表される．

問 4.44   点 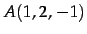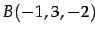$A(1,2,-1)$, $B(-1,3,-2)$ を通る直線の方程式を求めよ．

（答え）

Kondo Koichi
Created at 2003/09/09