Next: 4 初等関数 Up: 2 関数 Previous: 2 関数 Contents
3 関数のグラフ
![]() 軸と
軸と ![]() 軸を
直角に交わるように描き
軸を
直角に交わるように描き ![]() 平面 を用意する.
変数
平面 を用意する.
変数 ![]() の値を定義域内で変化させ,点
の値を定義域内で変化させ,点
![]() の軌跡を
の軌跡を
![]() 平面内に描く.
これにより関数
平面内に描く.
これにより関数 ![]() のグラフが得られる.
のグラフが得られる.
定義 2.3 (一価関数,多価関数)
ある一つの 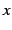 の値に対する
の値に対する 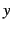 の値の個数で
次のように関数を分類する.
の値の個数で
次のように関数を分類する.
- 一価関数(single valued function)
 ある
ある 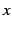 に対して
に対して 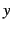 の値がただ一つ定まる関数.
の値がただ一つ定まる関数.
- 多価関数(many valued function)
 ある
ある 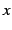 に対して
に対して  の値が複数定まる関数.
の値が複数定まる関数.
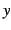 の値の個数が
の値の個数が 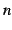 個となることが分かっている場合は,
個となることが分かっている場合は,
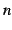 価関数(
価関数(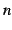 -valued function)と呼ぶ.
-valued function)と呼ぶ.
定義 2.4 (逆関数)
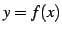 を方程式とみなし,
を方程式とみなし,
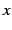 について解いたとき
について解いたとき  が得られたとする.
このとき
が得られたとする.
このとき 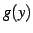 を逆関数(inverse function)
と呼び
を逆関数(inverse function)
と呼び
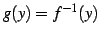 と書く.
変数の表し方が本質的でない場合は
と書く.
変数の表し方が本質的でない場合は
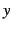 と
と 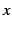 を取り替えて
を取り替えて 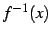 と書く.
と書く.
例 2.5 (逆関数の具体例)
関数
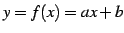 の逆関数を考える.
の逆関数を考える.
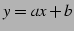 について解くと,
について解くと,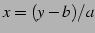 となるので,
逆関数は
となるので,
逆関数は
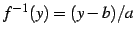 となる.
となる.
 と
と  を入れ替えると
を入れ替えると
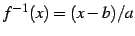 である.
である.
問 2.6 (逆関数のグラフ)
関数 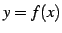 のグラフとその逆関数
のグラフとその逆関数
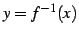 のグラフは,
直線
のグラフは,
直線 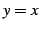 に関して線対称である.
これを示せ.
に関して線対称である.
これを示せ.
定義 2.7 (枝,主枝,主値)
多価関数が一価関数となるように値域を限定する.
このとき得られる一価関数それぞれを分枝(branch)と呼ぶ.
この分枝のうち代表する一つを
主分枝(principal branch)と呼ぶ.
主分岐は主値(principal value)ともいう.
例 2.8 (一価関数,多価関数,逆関数,分枝の具体例)
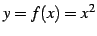 は一価関数である.
この関数の逆関数は
は一価関数である.
この関数の逆関数は
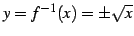 であり 2 価関数となる.
値域を
であり 2 価関数となる.
値域を  と
と  とに限定すると
一価関数が二つ得られる.
すなわち分枝は
とに限定すると
一価関数が二つ得られる.
すなわち分枝は
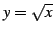 と
と
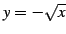 である.
である.
問 2.9
参考書(p.19)問題 2-1.
定義 2.10 (単調関数)
関数 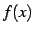 が
が
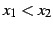 をみたす
任意の点
をみたす
任意の点 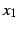 ,
, 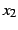 (
(
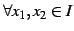 ) に対して
) に対して
-
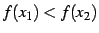 が成り立つとき,
関数
が成り立つとき,
関数 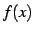 は単調増加(monotonic increasing)であると呼ぶ.
は単調増加(monotonic increasing)であると呼ぶ.
-
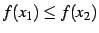 が成り立つとき,
関数
が成り立つとき,
関数 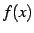 は
広義の単調増加(monotonic increasing in the wider sense)で
あると呼ぶ.
は
広義の単調増加(monotonic increasing in the wider sense)で
あると呼ぶ.
-
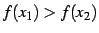 が成り立つとき,
関数
が成り立つとき,
関数 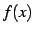 は単調減少(monotonic decreasing)であると呼ぶ.
は単調減少(monotonic decreasing)であると呼ぶ.
-
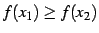 が成り立つとき,
関数
が成り立つとき,
関数 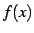 は
広義の単調減少(monotonic decreasing in the wider sense)で
あると呼ぶ.
は
広義の単調減少(monotonic decreasing in the wider sense)で
あると呼ぶ.
例 2.11 (単調関数の具体例)
関数 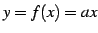 を考える.
を考える.
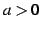 のとき
のとき 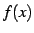 は
は
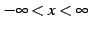 において単調増加である.
また
において単調増加である.
また 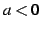 のときは
のときは 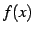 は
は
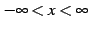 において単調減少となる.
なぜなら
において単調減少となる.
なぜなら
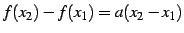 であり,
であり,
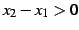 であることより,
であることより,
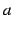 の符号により
の符号により 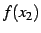 と
と  の大小関係が
定まるからである.
の大小関係が
定まるからである.
定義 2.12 (周期関数)
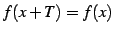 を満たす関数を
周期関数(periodic function)と呼ぶ.
を満たす関数を
周期関数(periodic function)と呼ぶ.
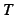 を周期(period)と呼ぶ.
を周期(period)と呼ぶ.
定義 2.13 (奇関数,偶関数)
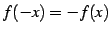 を満たす関数を
奇関数(odd function)と呼ぶ.
を満たす関数を
奇関数(odd function)と呼ぶ.
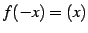 を満たす関数を
偶関数(even function)と呼ぶ.
を満たす関数を
偶関数(even function)と呼ぶ.
問 2.14
奇関数は原点に関して点対称のグラフとなる.
偶関数は 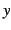 軸に関して線対称なグラフとなる.
これを示せ.
軸に関して線対称なグラフとなる.
これを示せ.
Next: 4 初等関数 Up: 2 関数 Previous: 2 関数 Contents
Kondo Koichi

Created at 2004/08/14