Next: 3 微分法 Up: 2 関数 Previous: 17 連続と不連続 Contents
18 連続関数
定義 2.71 (連続関数)
関数 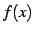 が定義内の任意の点において連続であるとき,
が定義内の任意の点において連続であるとき,
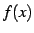 は連続関数(continuous function)であるという.
は連続関数(continuous function)であるという.
例 2.72 (連続関数の具体例)
次の関数は連続関数である.
| (168) | ||
| (169) | ||
| (170) | ||
| (171) | ||
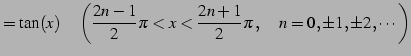 |
(172) |
定義 2.73 (閉区間における連続関数)
関数 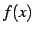 の定義域が閉区間
の定義域が閉区間
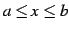 のとき,
その端点では条件
のとき,
その端点では条件
を満たすとき連続であるとする.
| (173) |
を満たすとき連続であるとする.
例 2.74 (閉区間における連続関数の具体例)
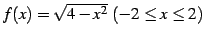 は連続関数である.
なぜなら
は連続関数である.
なぜなら
が成立するからである.
| (174) |
が成立するからである.
定理 2.75 (連続関数に関する性質)
関数 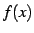 と
と 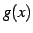 が連続関数のであるとき,関数
が連続関数のであるとき,関数
もすべて連続関数である. ただし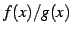 の定義域は
の定義域は 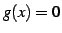 とならないものをとることにする.
とならないものをとることにする.
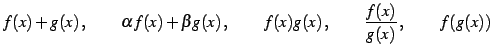 |
(175) |
もすべて連続関数である. ただし
例 2.76 (連続関数に関する性質の具体例)
巾関数 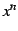 は連続関数である.
よって巾関数の線形結合である多項式
は連続関数である.
よって巾関数の線形結合である多項式
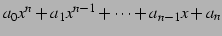 も
連続関数である.
も
連続関数である.
例 2.77 (連続関数に関する性質の具体例)
多項式
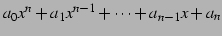 と
と
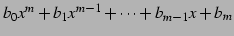 は連続関数である.
よってそれらの商である有理関数
は連続関数である.
よってそれらの商である有理関数
も連続関数である.
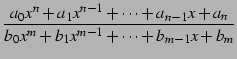 |
(176) |
も連続関数である.
例 2.78 (連続関数に関する性質の具体例)
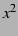 と
と 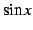 は連続関数である.
よってそれらの合成関数である
は連続関数である.
よってそれらの合成関数である 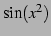 も連続関数である.
も連続関数である.
問 2.79 (連続関数の定義域)
次の関数が連続となる 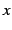 の範囲を定めよ.
の範囲を定めよ.
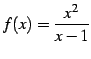 |
(177) | |
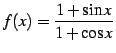 |
(178) | |
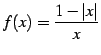 |
(179) |
Next: 3 微分法 Up: 2 関数 Previous: 17 連続と不連続 Contents
Kondo Koichi

Created at 2004/08/14