Next: 2 数列の極限 Up: 4 数列 Previous: 4 数列 Contents
1 数列
定義 4.1 (数列)
数列(sequence)とは数を順番に並べたものであり,
と書き表す.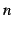 番目の数を第
番目の数を第 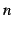 項と呼ぶ.
第
項と呼ぶ.
第 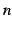 項を
項を 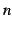 に関する式で
書き下したものを一般項(general term)と呼ぶ.
第
に関する式で
書き下したものを一般項(general term)と呼ぶ.
第 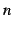 項,第
項,第 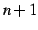 項,
項,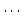 , 第
, 第 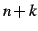 項の間の関係を書き下した式を
漸化式(recurrence relation)と呼ぶ.
項の間の関係を書き下した式を
漸化式(recurrence relation)と呼ぶ.
| (364) | ||
| (365) | ||
| (366) |
と書き表す.
数列についていくつか種類をあげる.
定義 4.3 (等差数列)
数列 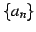 の隣り合う項の差が一定の数列を
等差数列(arithmetical progression sequence)と呼ぶ.
すなわち,漸化式と一般項とがそれぞれ
の隣り合う項の差が一定の数列を
等差数列(arithmetical progression sequence)と呼ぶ.
すなわち,漸化式と一般項とがそれぞれ
と表される数列を指す.
| (370) |
と表される数列を指す.
定義 4.4 (等比数列)
数列 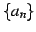 の隣り合う項の比が一定の数列を
等比数列(geometrical progression sequence)と呼ぶ.
すなわち,漸化式と一般項とがそれぞれ
の隣り合う項の比が一定の数列を
等比数列(geometrical progression sequence)と呼ぶ.
すなわち,漸化式と一般項とがそれぞれ
と表される数列を指す.
| (371) |
と表される数列を指す.
Next: 2 数列の極限 Up: 4 数列 Previous: 4 数列 Contents
Kondo Koichi

Created at 2004/08/14