Next: 7 項別積分 Up: 5 テイラー級数 Previous: 5 解析関数 Contents
6 項別微分
例 5.27 (項別微分の具体例)
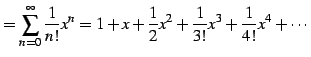 |
(659) | |
 |
(660) | |
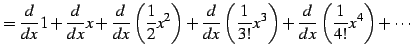 |
(661) | |
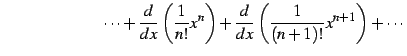 |
(662) | |
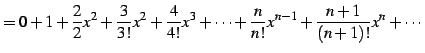 |
(663) | |
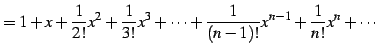 |
(664) | |
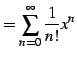 |
(665) | |
| (666) |
例 5.28 (項別微分の具体例)
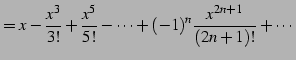 |
(667) | |
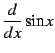 |
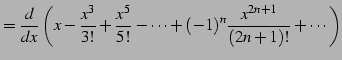 |
(668) |
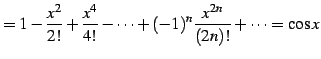 |
(669) |
例 5.29 (項別微分の具体例)
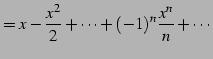 |
(670) | |
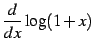 |
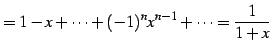 |
(671) |
問 5.30
これを示せ.
例 5.31 (テーラー級数の微分)
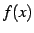 に関するテーラー級数を微分したものは,
に関するテーラー級数を微分したものは,
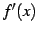 に関するテーラー級数となる.
テーラー級数は微分演算に対して不変である.
に関するテーラー級数となる.
テーラー級数は微分演算に対して不変である.
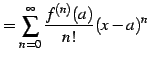 |
(672) | |
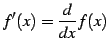 |
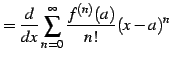 |
(673) |
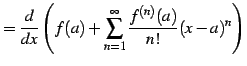 |
(674) | |
 |
(675) | |
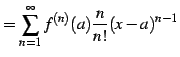 |
(676) | |
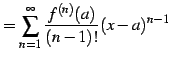 |
(677) | |
| (678) | ||
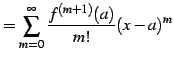 |
(679) | |
| (680) | ||
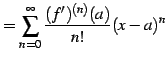 |
(681) | |
| (682) |
Next: 7 項別積分 Up: 5 テイラー級数 Previous: 5 解析関数 Contents
Kondo Koichi

Created at 2004/08/14